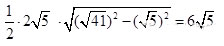例题:
分析
本题考察是是根据三视图求几何体的表面积,几何体的表面积,同学们都知道,关键是还原出几何体,把每个面的面积求出来再相加即可,但这题的关键是,如何还原?还原出的三棱锥是什么样的呢?我想象不出来!所以,题目也就解不出来!接下来,老师带同学们一起回顾一下,如何通过三视图还原几何体!
回顾
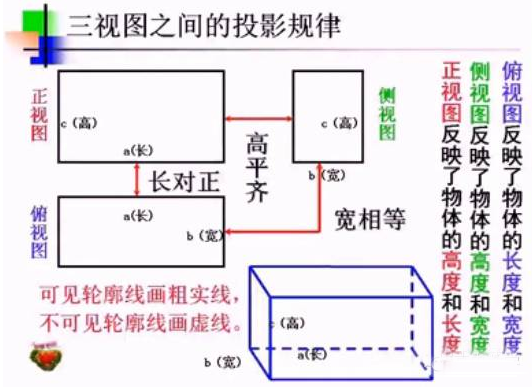
1、 三视图是怎么来的?
三视图可以看作是观测者从上面、左面、正面三个不同角度观察同一个空间几何体而画出的图形。
2、 三视图的性质:
主俯一样长,主左一样高,俯左一样宽,或者也可以说是长对正,高平齐,宽相等,这三句话是什么意思呢?跟老师一起看一下下面的图形。
3、 如何还原直观图?
一般情况下,我们高中阶段的三视图是比较简单的,大多数通过对长方体或者正方体进行切割而成,或者是圆锥(或圆柱)与长方体(或正方体)的组合,所以,同学们要对我们学过的最基本的几何体的三视图熟练掌握,例如,三棱锥,三棱柱,圆柱,圆锥,四棱锥,四棱柱等。
老师通过对近三年高考题及模拟题的统计,发现有这么一个规律:
(1) 如果三视图中有两个或三个三角形,那么这个几何体一定是棱锥;(这种考的是最多的)
(2) 如果三视图中有一个圆,那么这个几何体可能是圆柱或圆锥,另外两个图要是三角形,那一定是圆锥,如果是长方形,那一定是圆柱;
(3) 如果三视图中只有一个三角形,那么这个几何体很有可能是三棱柱,此时要注意株的摆放形式,有可能是放倒的三棱柱!
当然,上面老师说的是一些比较简单的,如果碰上麻烦的,我根本就看不出来的,更甭提还原了,怎么办呢?老师推荐一个方法:嵌套法。
嵌套法,指的是根据三视图,把三个视图嵌套到长方体或者正方体中,然后再把多余的线擦掉,即能画出所要求的几何体。一般情况下,我们只需要在长方体(正方体)中找到这个几何体的顶点即可。
这么说,同学们可能不是特别明白,下面老师通过今天的例题,给大家解析清楚一点。
解析
按照老师刚才说的方法,我们利用嵌套的方法对此三视图进行还原。
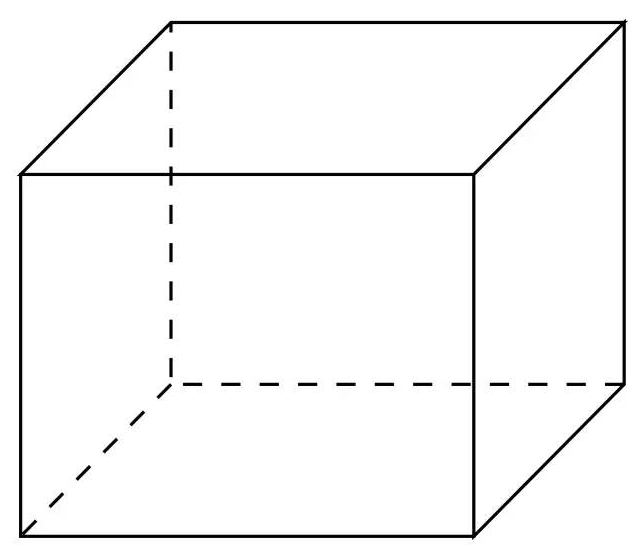
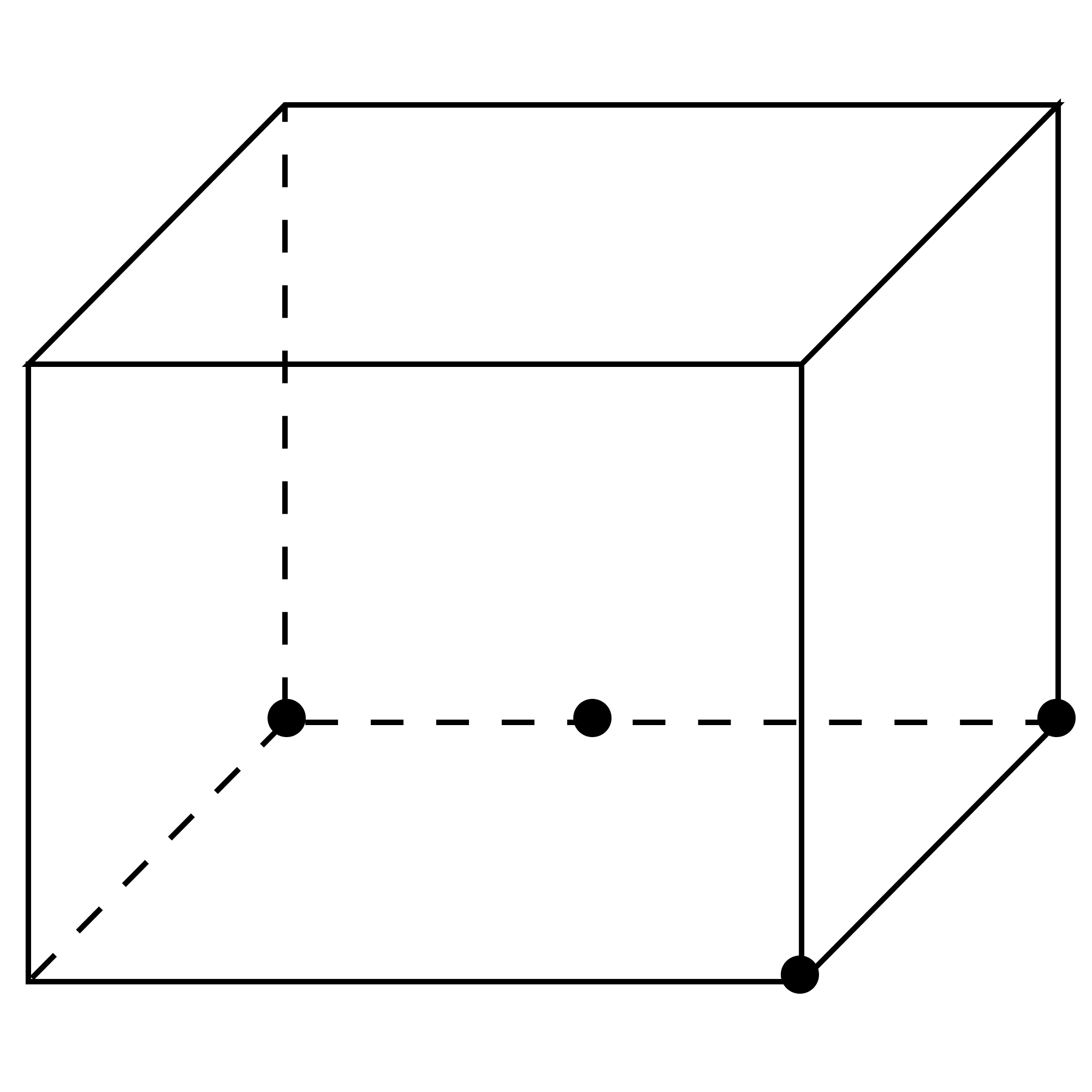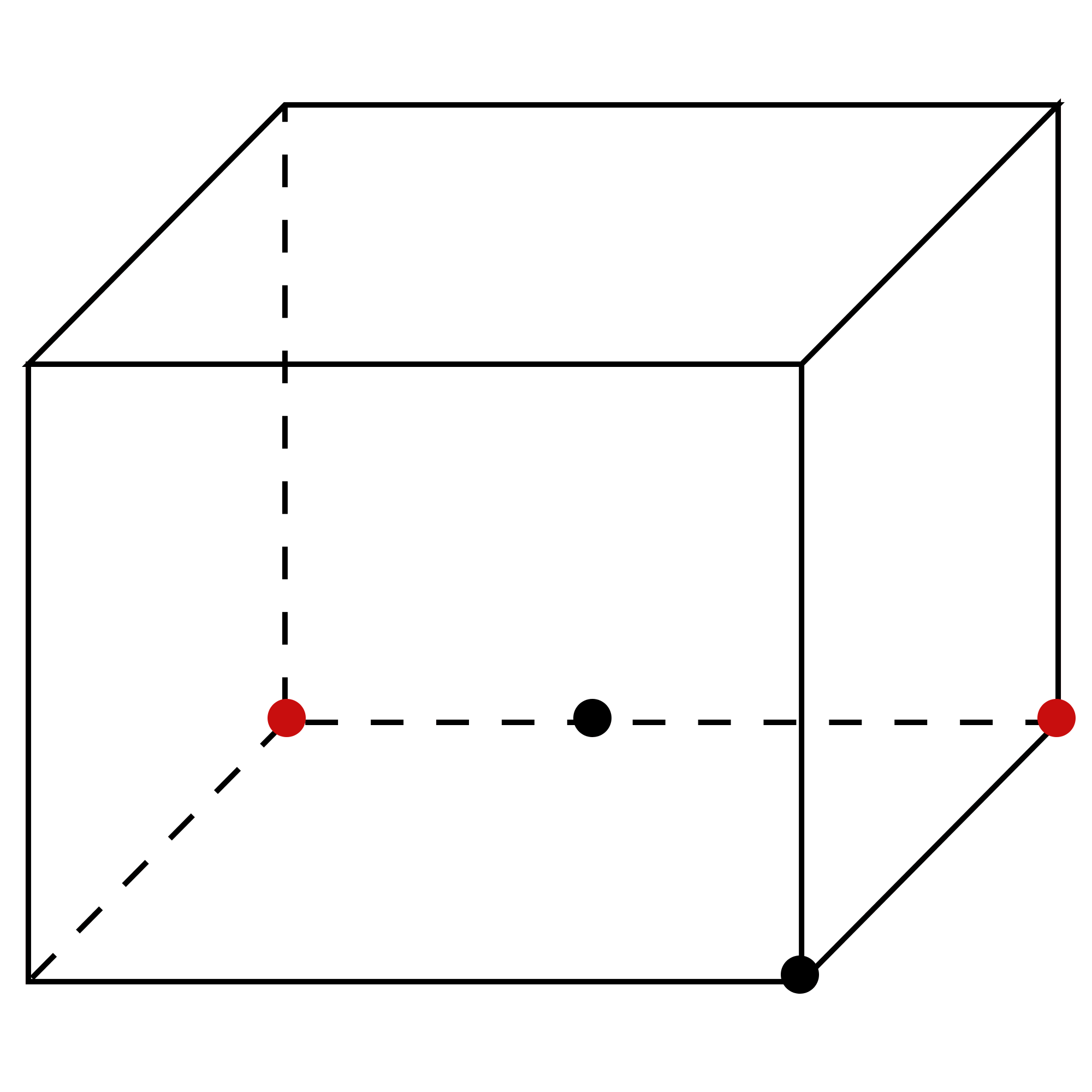
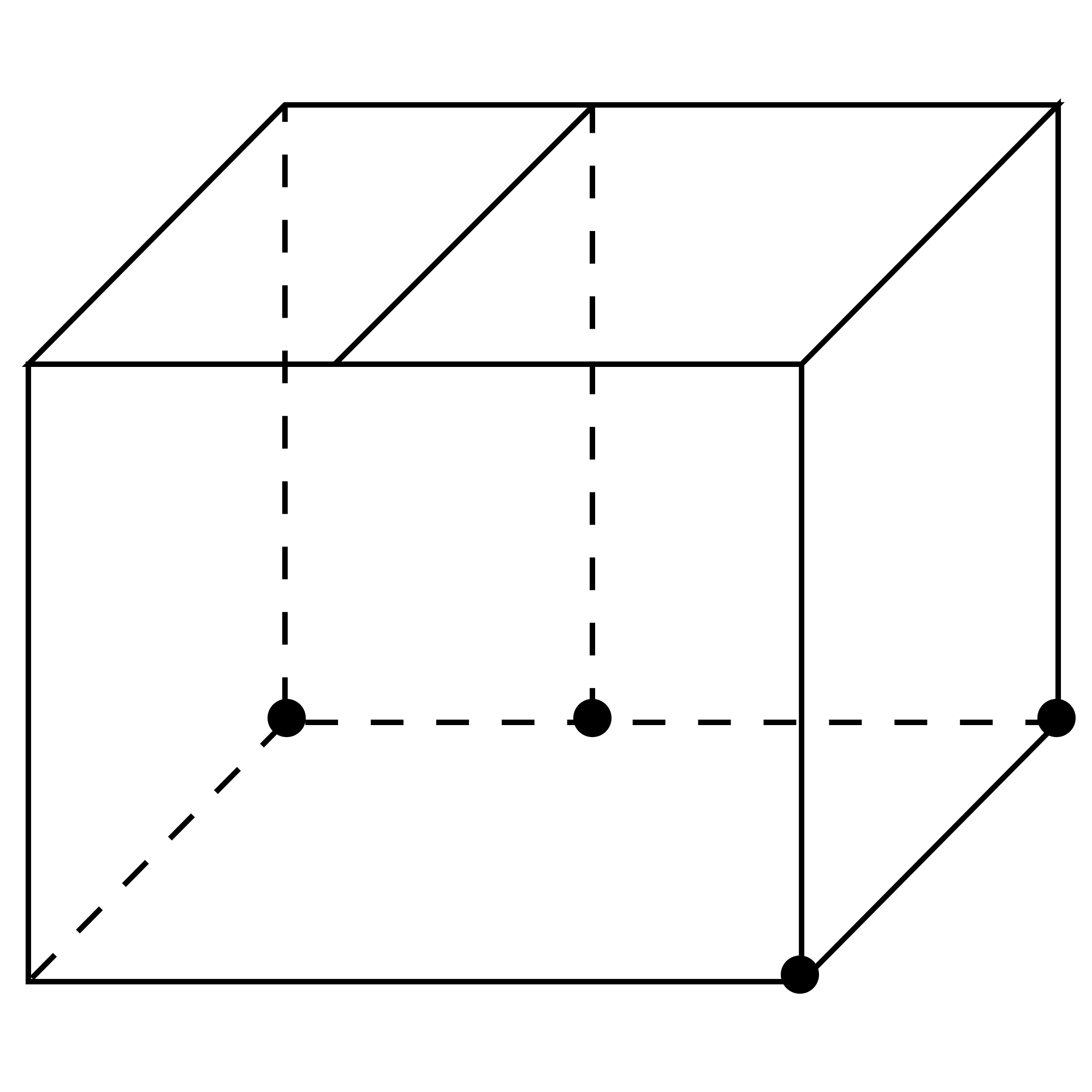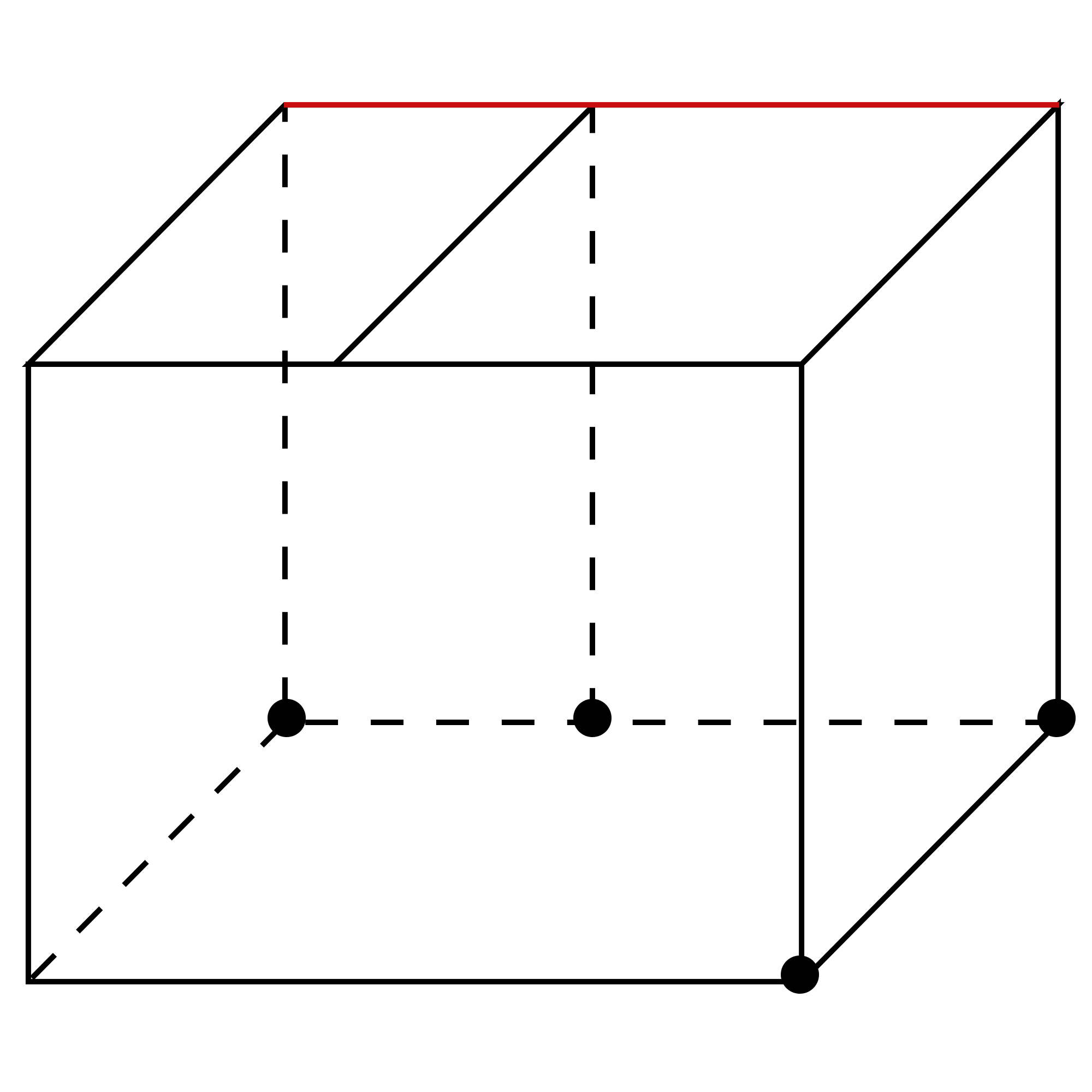
首先,通过主视图与左视图的底边,我们选择长方体进行嵌套,长方体的长为5,宽和高均为4,如图:
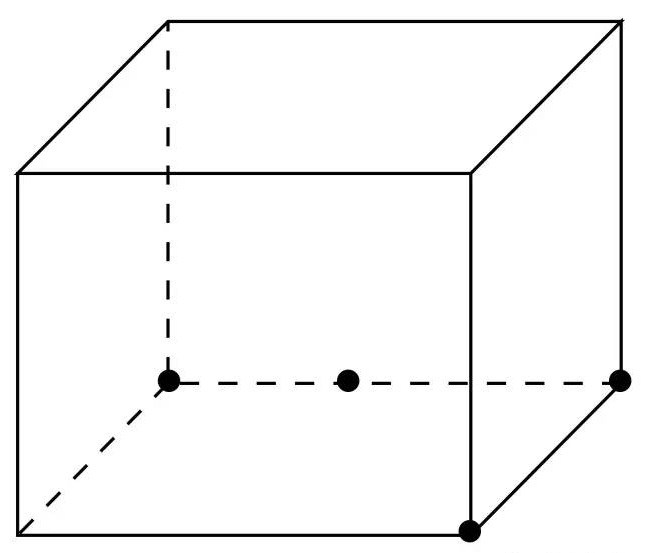
其次,观察俯视图,俯视图是一个直角三角形,中间还有一条线,根据此直角三角形的形状,所以俯视图应该嵌套到长方体的底面上,如图找到点:
然后,观察主视图,是一个三角形,其中三角形的顶点与底边标记2的那个点的连线与底边应该是垂直的。因为主视图是在几何体前方观察几何体所得到的图形,再根据俯视图找到的点,可以确定,主视图的底边应该与俯视图的边是一条,所以如图找到其在长方体中的两个点,
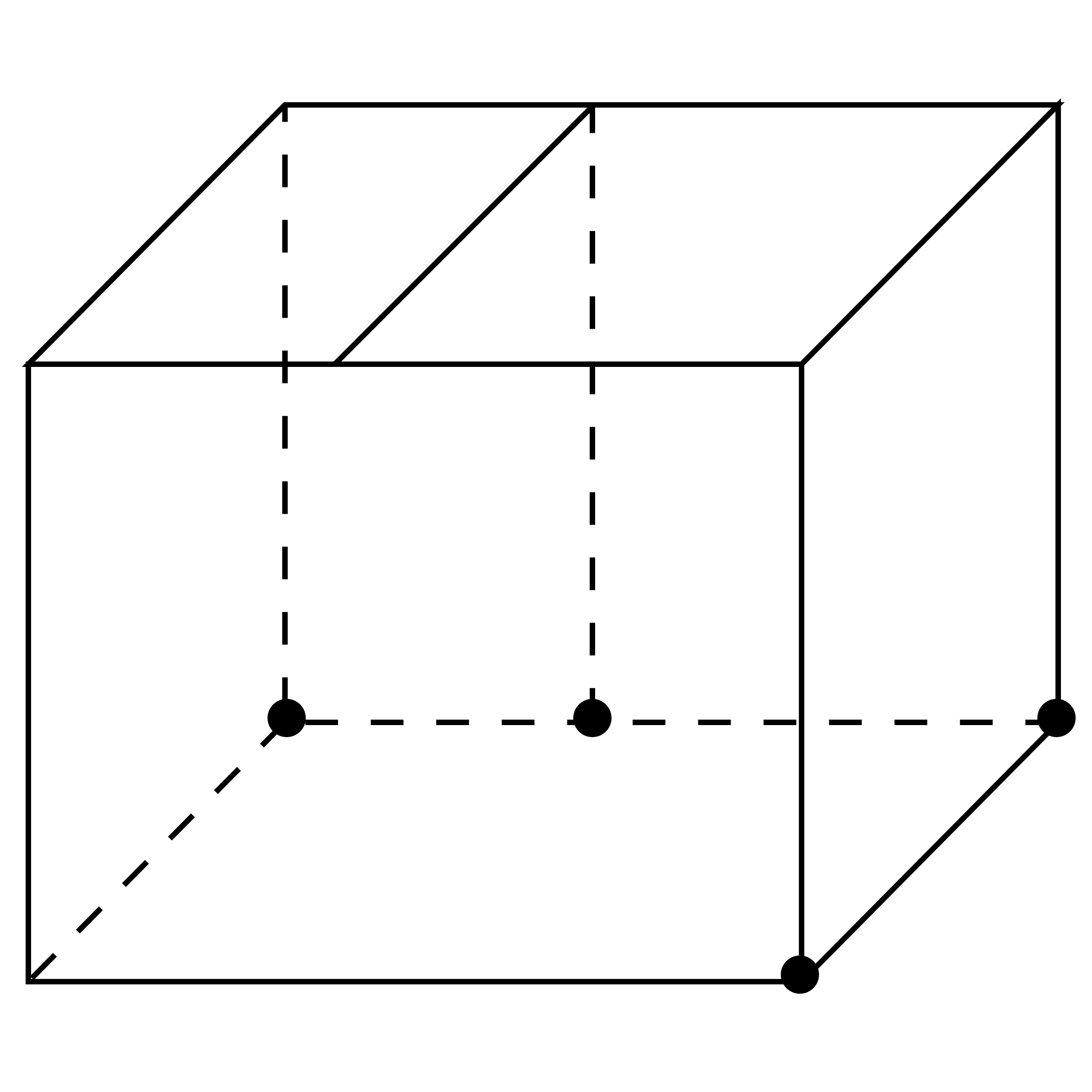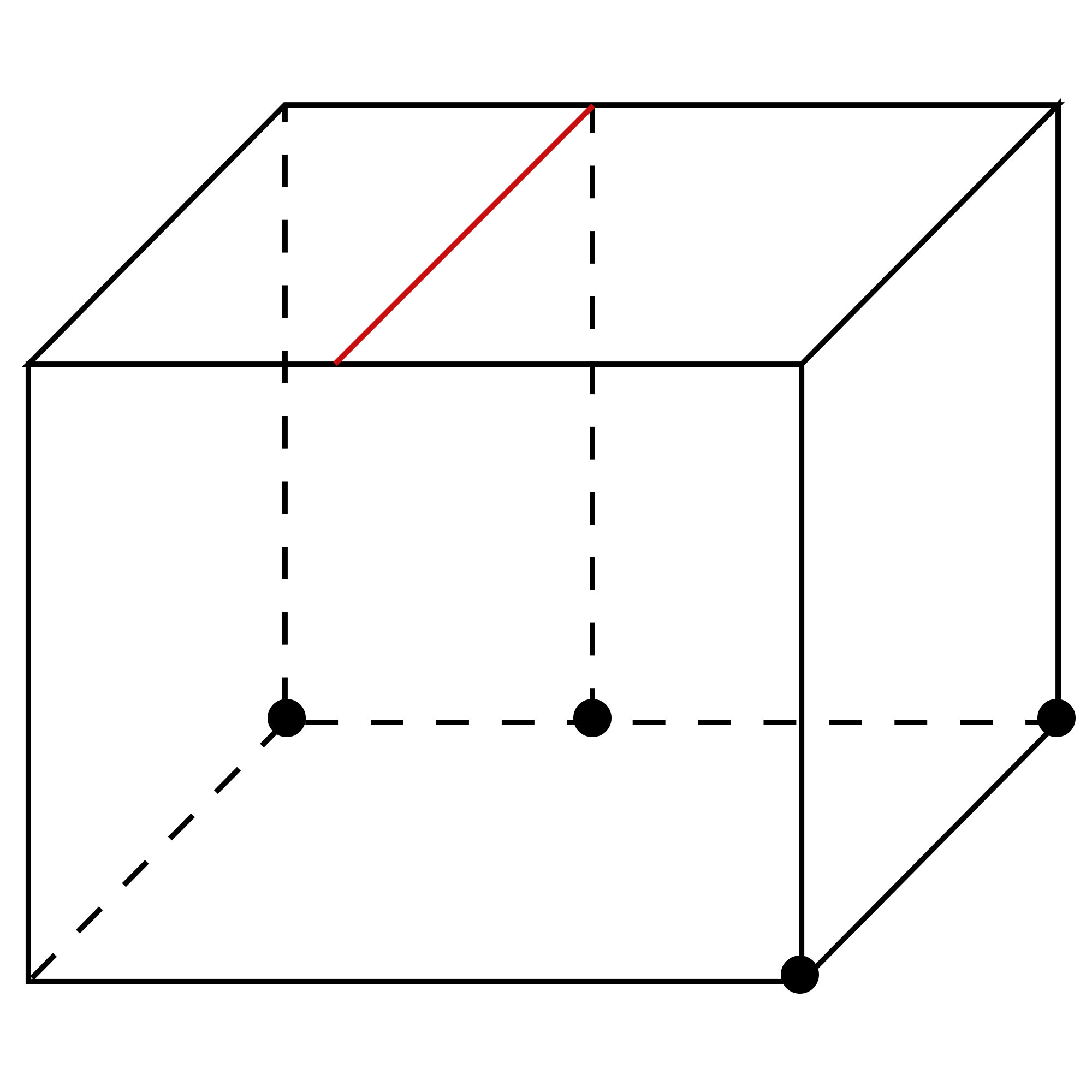
然后再确定主视图这个三角形的顶点在那个位置,根据刚才说的三角形的顶点与底边标记2的那个点连线与底边垂直,所以顶点可能在长方体的这一条线上,如图:
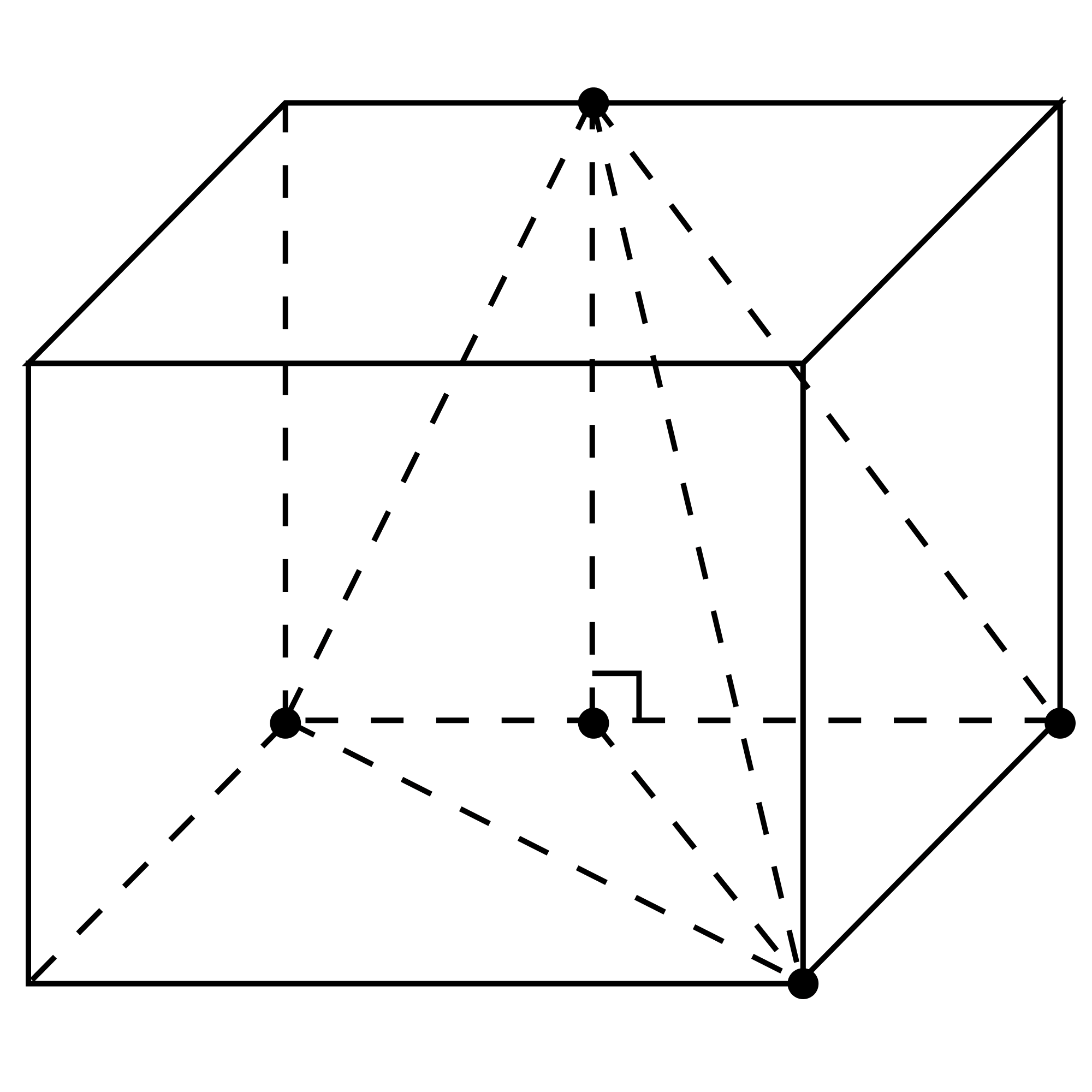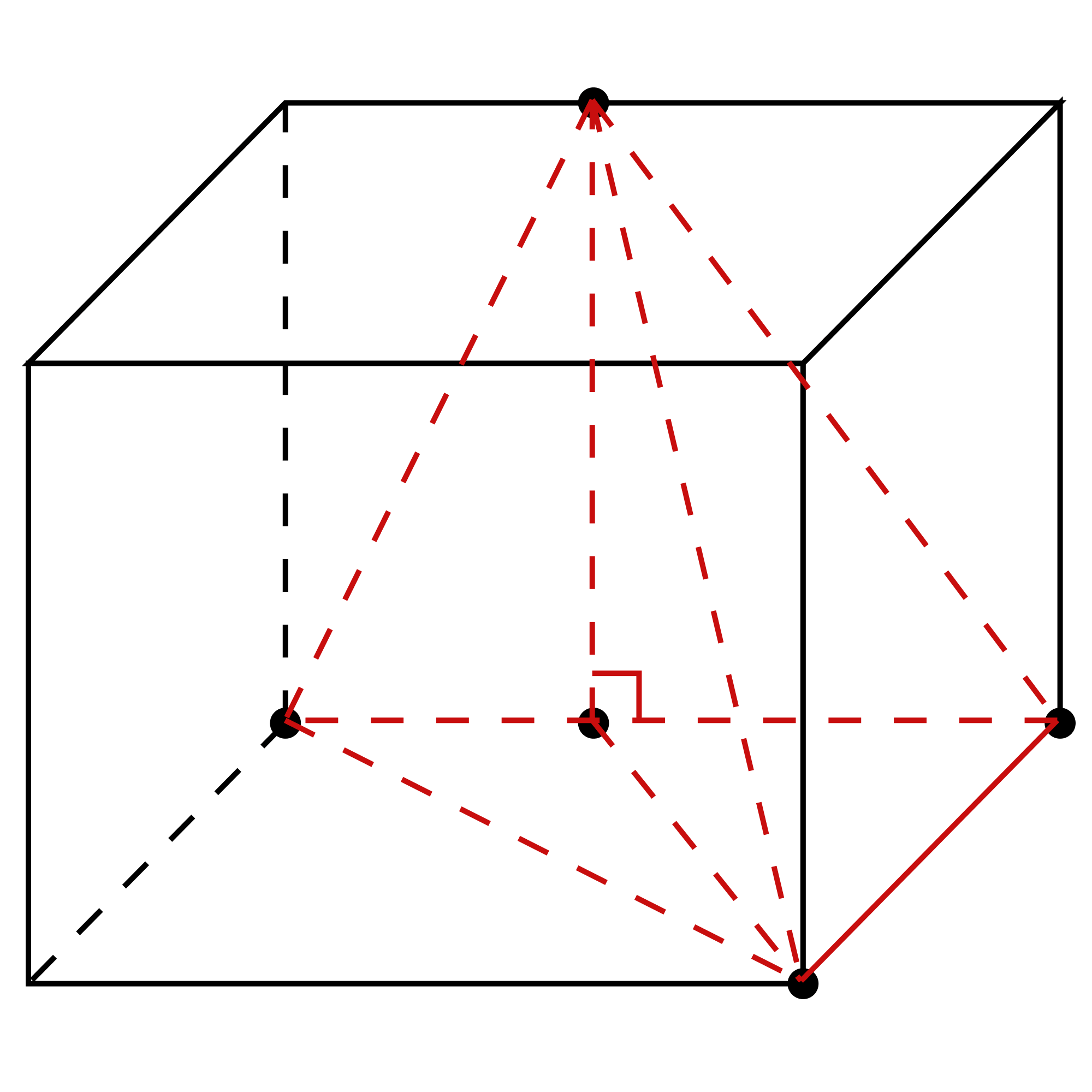
紧接着根据左视图找顶点的位置,应该在如图的这条直线上,
最后,通过这两条直线相交得到这个三棱锥的最后一个点,然后把4个顶点连接,如图:
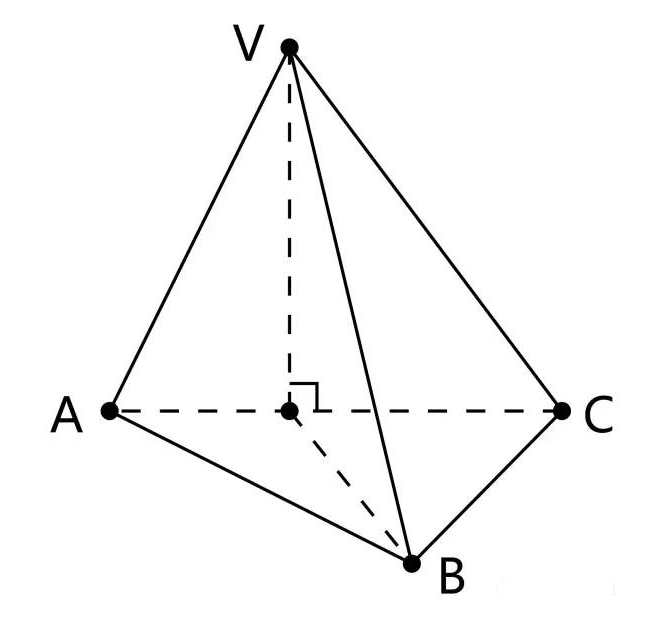
最后的最后,把外面这些不需要的线擦掉,然后几何体就出来了,如图:
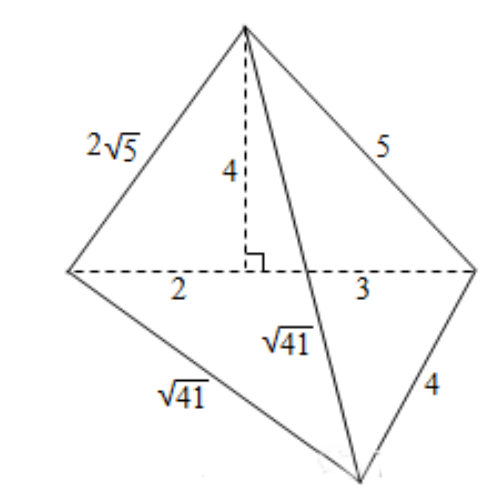
根据三视图的性质,可得:AC=5,BC=4,高h=4,并且边BC垂直于AC,所以三角形VBC也是直角三角形,即BC垂直于VC,(同学们可以根据刚才的条件自己证明一下)
三角形VAC的面积=1/2*5*4=10
三角形VBC的面积=1/2*4*5=10
三角形ABC的面积=1/2*4*5=10
三角形VAB的面积=
最后,把4个三角形的面积加起来可得结果,最后选择B.