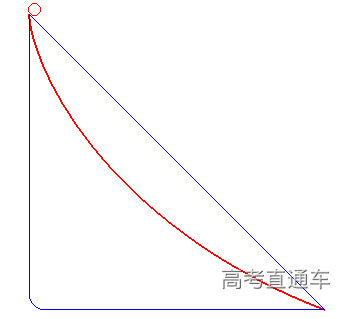
导读
在今天刚刚结束的自由式滑雪女子大跳台决赛,谷爱凌夺得金牌!这一刻,是谷爱凌自己获得的首个冬奥会奖牌,也是中国运动员第一次参加冬奥会大跳台的比赛!
如何从物理理论的角度来降低滑雪时间。
大家考虑一下,如果a点有一个球滑落到b点,哪一个曲线最快呐?
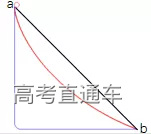
一起来看看示意图↓↓↓
到这里就会有很多的小伙伴可能想起来:呀,我知道哦,我听说过,这是最速降线!但这背后蕴含的物理你真的知道吗?
首先介绍一位伟大的人物-费马,对他的介绍是这样的:一位律师,一位业余数学家和一位业余物理学家。1662年,作为一名“业余家”, 费马提出费马原理:光传播的路径是光程取极值的路径即光走过的路径是用时最少的路径。
费马原理能够导出三个几何光学定律:1,光沿着直线传播;2,光的反射定律;3,光的折射定律。
如何用费马原理证明光的折射定律?
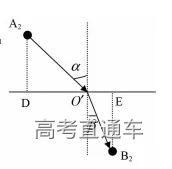
如上图,—束光由A2界面透射到达B2点,设光在界面上方速度为v1,下方速度为v2,A2D=h1,B2E=h2,DE=l, DO’=x,列出时间方程。
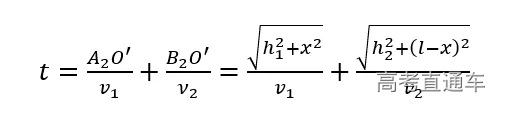
根据费马原理,时间t应取极小值,对上述方程取微分得。
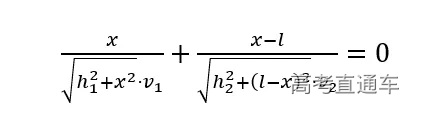
将该方程化简。
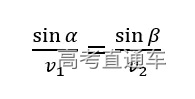
得证√
(这一个原理不仅对光学的理论发展做出了非常大的贡献,更对数学中变分法和物理学中最小作用量原理的发展起到了先驱的效果。)

图片来源|百度百科:费马个人像
那有小伙伴要问了?为什么提到费马呐,这是因为最先解决最速降线问题的约翰·伯努利就巧妙的借鉴了费马原理。
他把运动的小球想象成一束光,光不断的通过不同的介质,光是聪明的,它会走时间最短的路线,将每层的厚度无限地变薄,则球的实际运动与光的传播就会无限的接近,而最终光的传播路线就是我们想知道的最速降线!
伯努利想法的最速降线方程的证明也不能少。
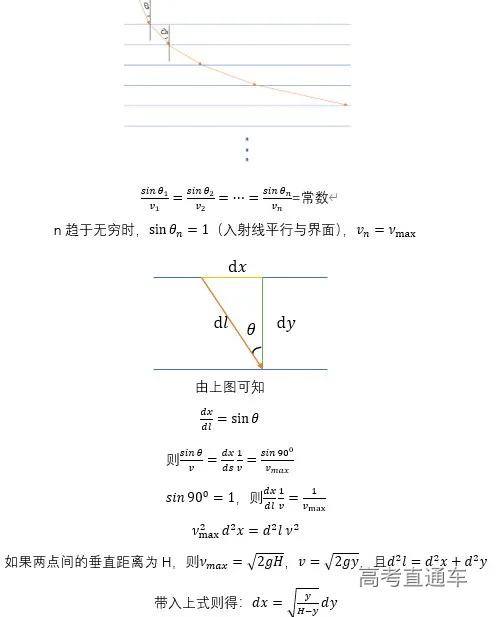
得证√
看到这里不知道大家对最速降线的理解有没有提升了一个档次呢(学会暗示:其实你学会了)。
接下来是目前最"常规"的解法:将运动方程表达成泛函形式然后通过变分法中欧拉方程的第二形式求解。
现在告诉你,你已经掌握了滑雪的最佳秘籍,提前踩点,找到雪道上的最速路线,你就是人群中最靓的仔。最后祝我们的参赛冬奥健儿们不留遗憾,胜利凯旋!