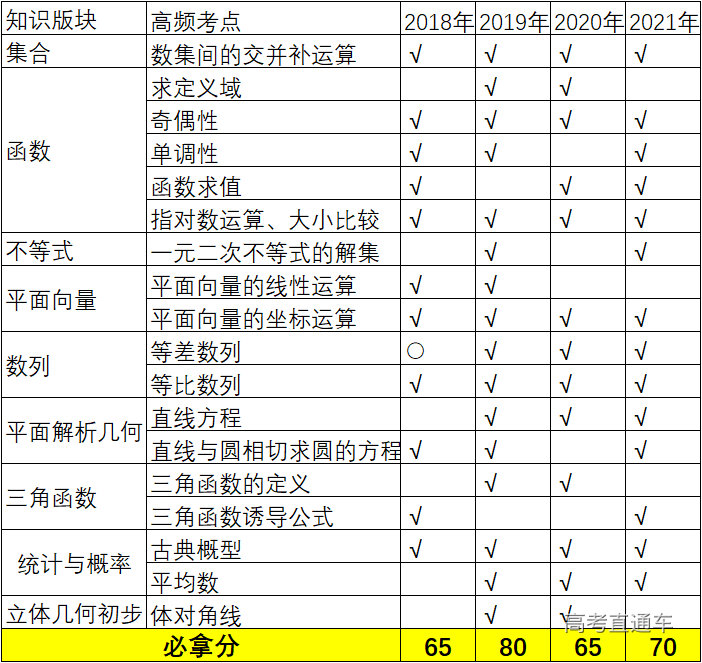
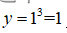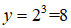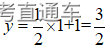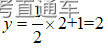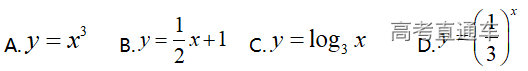春季高考的备考一定要做模拟卷或真题卷的整卷训练，查漏补缺，分析试卷情况找出自己的弱项，针对性重点复习。如果基础太薄弱怎么办？敲黑板啦！！！基础薄弱的同学怎么考好数学，就看这篇干货了！
必拿分题主要分为以下两大类题型，下面分别举例讲解一下这大两类题型的解题技巧，告诉大家怎样更好得分：
公式背诵计算类：
包括指对数运算、函数奇偶性、解不等式、平面向量的线性运算、数列、求直线斜率、三角函数相关公式、体对角线的计算
这类题型只需把相关公式牢记于心，答题时套公式计算，如：
（1）指数运算：背诵公式，套入计算。
（2）函数的奇偶性：判断函数奇偶性可以直接代入公式：
符合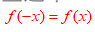
符合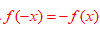
（1）指数运算：
【解析】直接套上面公式⑥可得，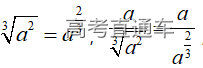
（2）函数的奇偶性
（2021年真题）下列函数为偶函数的是（ ）
，
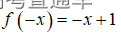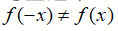，不是偶函数；对选项B，
，
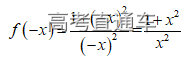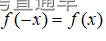，是偶函数。这类题题型需在理解基础概念的基础上运用求解，一般考查形式单一直接，可直接记忆口诀，如：
（1）数集间的交并补计算：记口诀“交集开口向下取相同，并集开口向上取全部，补集大C取没有”
（2）求函数定义域：
记三种特殊函数定义域即可：（1）分数函数分母不为零；（2）偶次根式函数被开方数大于等于零；（3）对数函数真数大于零；
（3）函数的单调性：记口诀：“x大y大为增，x大y小为减”，做题直接代数字计算即可。
（1）数集间的交互补计算：
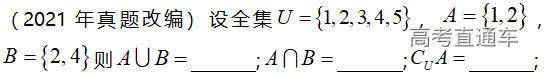
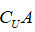符号类似大写字母C表示求全集U中A没有的部分，取全集U中有而A没有的所有的元素：3,4,5；即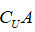={3,4,5}。（2）求函数定义域：
①分数函数分母不为0：
例：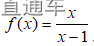
②偶次根式函数被开方数大于等于零
例：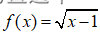
③对数函数真数大于零
例：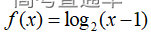
（3）函数单调性
（2021年真题）下列函数在其定义域内为减函数的是（ ）
【解析】减函数要求x大y小，直接代入数字，例如对选项A，代入x=1计算得
