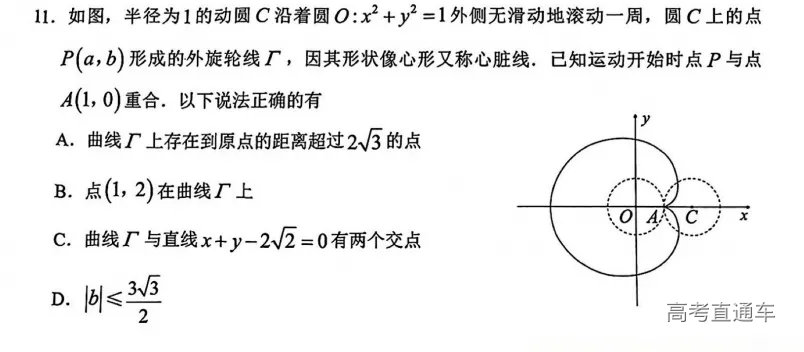
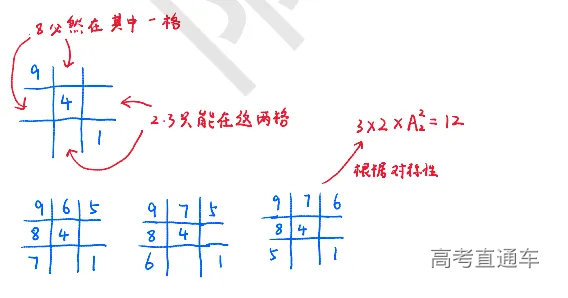
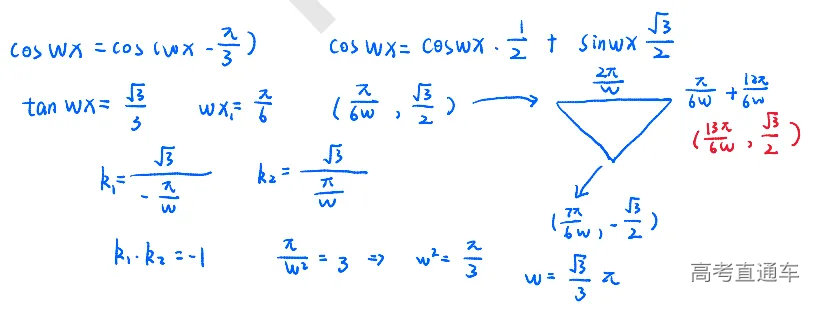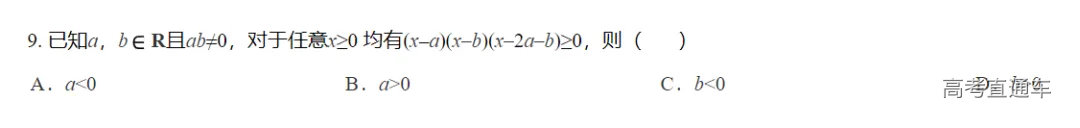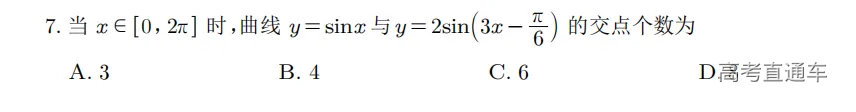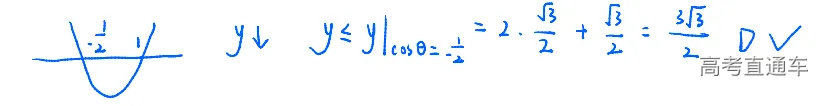广州一模试卷很新，难度很大，看似十分创新的题目，基本上都很经典，这也符合了现在的高考命题趋势。如果有认真研究近10年高考真题的同学，肯定不会对一些题目陌生。下面让我们一起来看看这份试卷是怎么从经典中创新的。
试题分析与解析
【T1-T4】
【分析】前四题简单给大家说说，就不写解析了。第一题考查复数的运算，注意题目问的是虚部，虚部没有i。第二题考查集合的运算，对于一些基础不扎实都同学可能就选C了，这道题一定要注意子集和真子集符号的区别。第三题是简单的向量运算感觉是没有什么难度，把对应量表示出来，代换就行了。第四题考查圆台侧面积公式（推导过程可以见: 24届金丽衢十二校第一次联考，这合理吗？）。感觉好久没见模拟卷考这个公式了，帮大家复习复习挺好的，但其实不知道这个公式也没事，可以自己推，用两个圆锥侧面积来减。
【T5】
【分析】 本题考查双曲线离心率的计算，这道题如果知道二级结论可以秒，不知道的话我们可以简单算一下，计算量也不大。先设出两条渐近线 转化为标准形式 ,设p点坐标,用点到直线距离公式，乘一下就出来了。当然作为选择题，我们可以找特殊点顶点，这样这题就很快了再利用渐近线斜率为b/a就能推出顶点到渐近线距离又由于对称性距离是一样的，很方便。
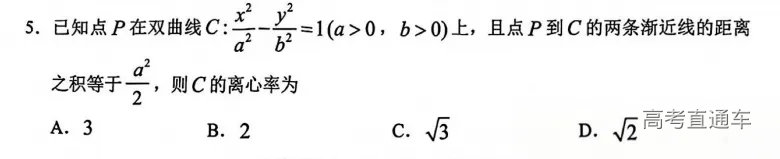
【解析】
【T6】
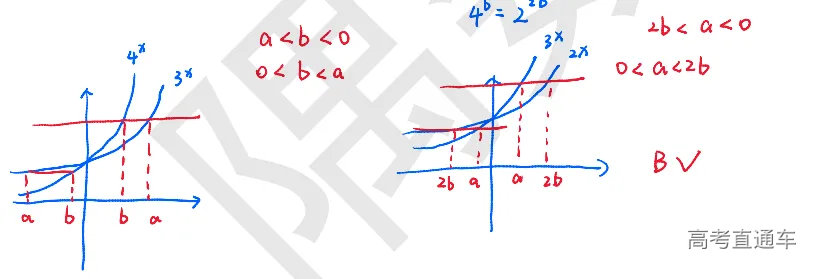
【分析】 本题的关键是数形结合，我们现在坐标系中画出，在令他们等于同一个值，即一条直线与他们相交，交点的横坐标就是 a，b对应的值。这样就很容易判断出来A和C都是错误的。后面分析a和2b ，4容易让大家想到2的平方，所以我们简单变形一下 ，再画图像就可以分析了。
【解析】
【T7】
【分析】 第七题有点小难度，重点是大家能先找到他们交点对应的值，先把式子展开，可以求出来tanwx的值，根据这个值和周期，我们去找出3个交点，再利用斜率关系或者向量表示他们之间的垂直关系即可。
【解析】
【T8】
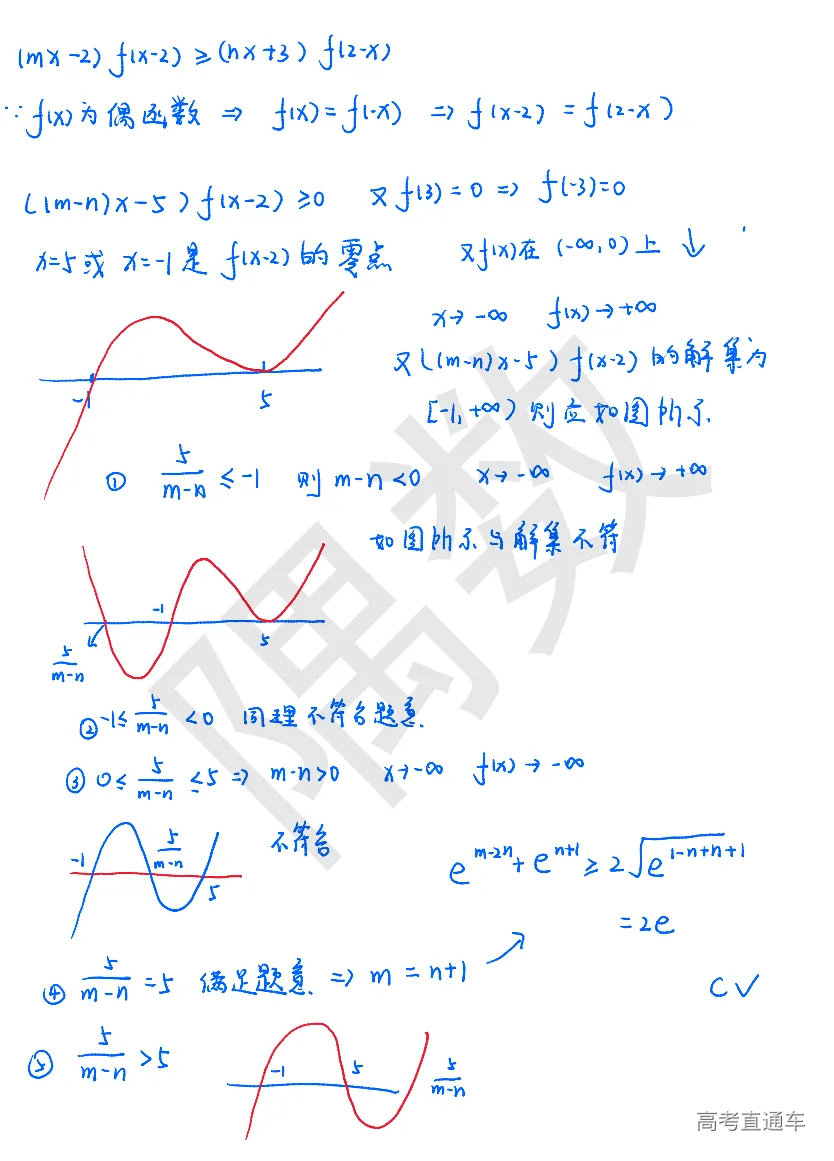
【分析】第八题，选择题部分我非常喜欢的一道题，这道题不仅考查了基本不等式的运用，还考查了模拟卷出现频率不算高的“奇穿偶回”，特别经典的一类题目，我们先根据偶函数的性质把代换掉，方程最终形式变为,下面就是根据零点讨论图像的变化，找到符合题目的图像。画图的过程就好像穿针引线!这种题目非常的经典！2021年的全国乙卷中就考过这么一道题，当然还有2020年的浙江卷，广州一模很巧妙的把这类题结合函数的性质改编，我觉得出得是很好的。下面把浙江卷和全国乙卷这两道题留给大家练习。本周限时训练会再给大家做一道！其实本次广州一模还有一道题跟2020年浙江卷有点关系，我们后面说。
【2020年浙江卷】
【2021年全国乙卷】
【解析】
【T9】
【T10】
A选项我们先求导函数，根据极值点的导函数值为0，求出a，B选项我们根据导函数得出x在（0,1）区间上是小于0，这意味着f（x）再这个区间上单调递减，而x∈（0,1）时$x^2f(x)$,B选项错误，这道题是有一点真题的味道的，C选项我们可以先对原函数求导，求完再把2+x和2-x带进去发现是相等的，C选项正确。D选项就涉及到上面放的真题中，函数中心对称的性质了。
【解析】
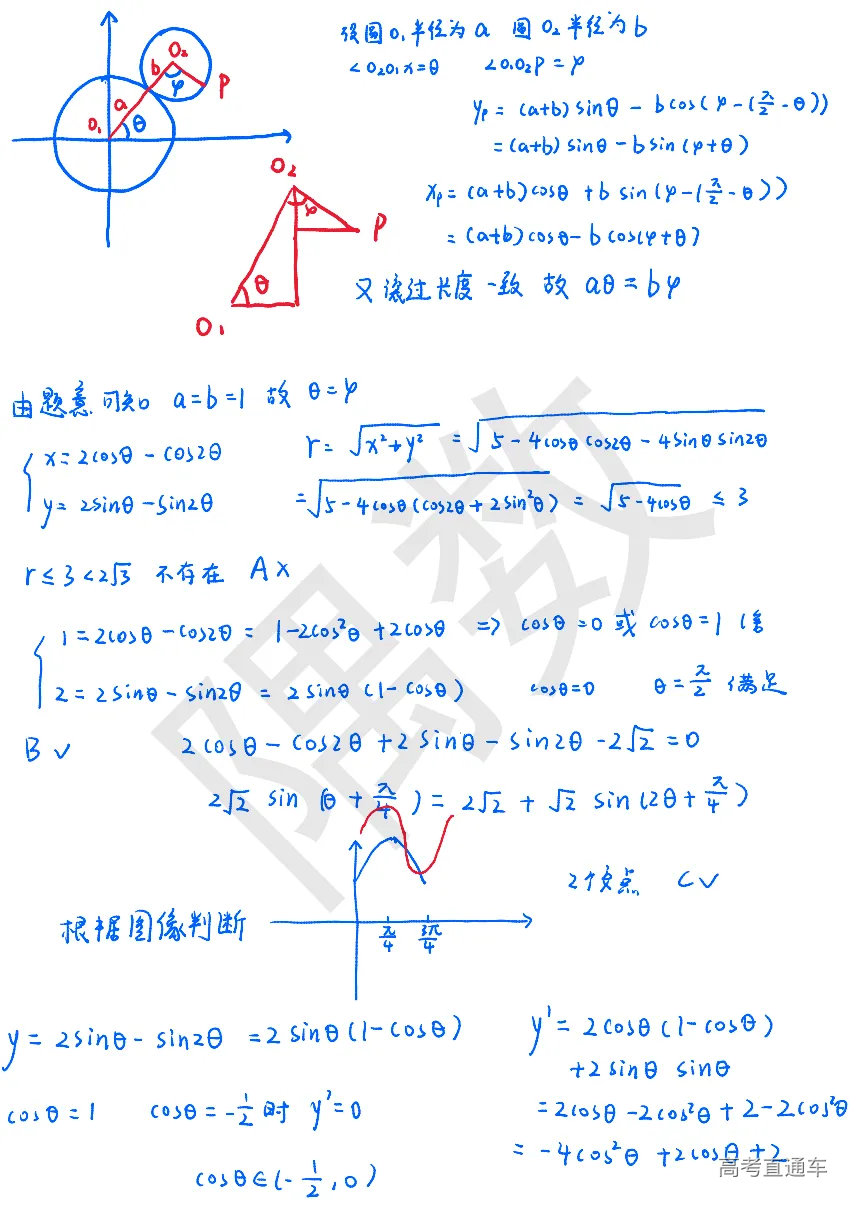
【分析】 说实话，我觉得这道题对大家来说是不友好的，曲线方程没给大家，大家并不会推导，而这个推导过程，是数学专业解析几何教材中的一道课后习题，不过真的要推导起来也不难，我们先画出两个圆，再设两个角，先表示出P坐标，再通过滚过的长度一致得到：aθ=bφ， 由于题目给的a=b，所以θ=φ，这样我们就得到了P的坐标参数表达，后面就是对选项的逐一分析，A选项实际上就是OP长度的取值范围，我们通过计算化简可以得出来，不存在这样的的点，B选项要注意不能因为我们这个设的是参数方程，所以看到点（1,2）去求正余弦，然后代入看对不对，因为我们这个参数方程所设的θ不是OP与x轴所成角！，所以要从结果推θ存在不存在。C选项讲坐标代入，变成了函数交点问题，需要画图形，又把人拉回到了2024年新高考I卷的这道题
D选项模拟卷天天考的三角最值问题，想必大家应该没啥大问题吧。
【解析】
【T12】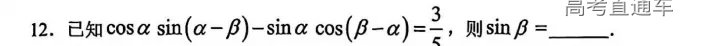
【T13】
【解析】
【T14】
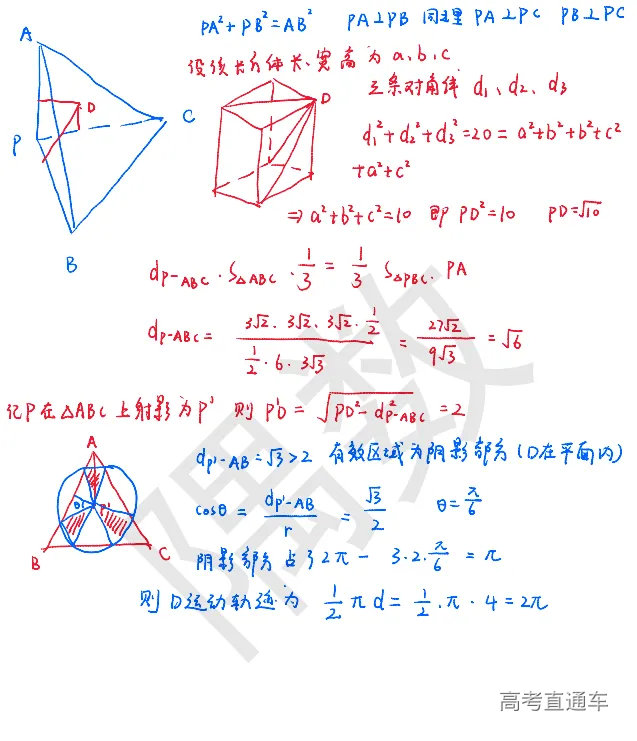
【分析】这道题很巧妙的地方在于，这是一个三条边，两两相互垂直的三棱锥，根据这个性质我们过D做各边的垂线，再对D作垂直面PBC的高，很容易证明他们构成一个长方体，再根据题目给的条件，建立等式，算出来DP的值，DP是定值，轨迹自然就知道了，是一个圆，我们求出P到面ABC的距离，算出圆半径 ，最后求求D在ABC内部的轨迹。其实最后这个问题的回归，很多模拟卷都考过，比如金丽衢期末考（2023年1月金丽衢十二校第一次联考高三数学）、再比如浙南名校联考
不过这道题，最难想的是前面一步，如何用好到三边距离和为定值。这道题如果选用建系的方法，计算量很大（中间要用到向量叉乘的几何含义），但是最后也是能求出来这个圆的方程的。
【解析】
【T15-16】
【T17】
【T18】
【T19】
