作者:余正熙@从容有数
单选:都能看出来原型,都是高考真题改编,都有创新。
6改编自高考真题,指对互化是这类问题的典型解法,在这里尽显优势;
7正弦型,换元后算坐标直观一些,图像实际上是等腰直角三角形;
8图像分析结合穿根法,m-n=1,这也算是一个易错题:5是零点,而不是-1。
多选:计算量上来了,除了基本功,也考验临场应变,比如11C实际上不用算。
10对称性,原函数的中心对称、导函数的轴对称,D选项用对称性就够了,如果是导数解答题,还可以升级为拐点偏移,再上点强度;
11心脏线,这种旋转问题去年的试卷精讲讲过,写对参数方程就万事大吉了,不过命题人还是很友善的留了个A选项,三角不等式就能排除它——其他全对,就看你敢不敢猜。BD用参数方程正面求解,C不需要联立,带入B的(1,2)即可确定直线与曲线是相交的。
2023年12月云南省云南师大附中诊断联考:
填空:不仅有计算量,还有巧劲,立体几何这个与2022届武汉调研考的那个填空压轴有点神似,只是没有多动点,所以没有那么丧心病狂。
13计数原理,穷举+剪枝,2024届临沂一模单选压轴题和这个有点类似。
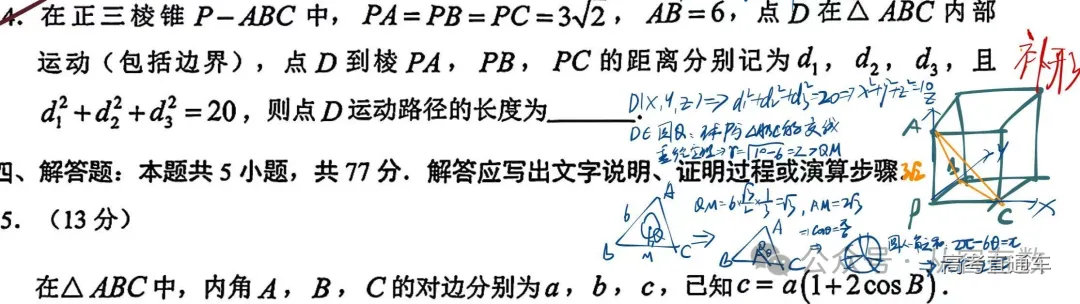
14立体几何动点轨迹,补形正方体后,D点轨迹就是球面与正三角形截面的交线,垂径定理很容易确定半径,注意这不是完整的圆周,需要耐心计算圆心角。
解答:前两题开足马力送温暖,后两题撤回了一点暖气,结果是冻得梆硬。
17条件概率、马尔科夫链,就是有点抽象,既有k又有n,大部分人到这里应该都耗尽心智了,考后再动笔试试看,其实没那么难——第三问有bug,这个系数小于1,一眼就能秒杀,都不需要展开,从这个细节来看,这张试卷的工期似乎有点仓促。
18圆锥曲线+三次函数,很多人可能会疑惑导数解答题去哪里了,就在第三问。平行的证明是送分题,估计大部分人在考场上都止步于此。第三问,面积的计算肯定存在多解,最优策略是转化为与三角形OAB的比值,正好可以用截距,连韦达定理都不需要,注意四次方程可以猜根y=-2,从而降幂为三次方程,导数这部分没有任何挑战,三次函数是单调递增的,二分法确认零点唯一即可,前面我写了对称性,所以零点唯一对应直线唯二。
19反函数+莫比乌斯函数,第一问送分,第二问可以证明函数单调且与y=x不相交,因此不成立,第三问可以先猜等比数列,再扩展到莫比乌斯函数,接下来f(x)的构造就很明显了。
对于考生来说,如果仅仅盯着参考答案,误以为这些“华山一条路”是开天眼的结果,那么这些试卷的良苦用心就白费了。除了少数难度过高的19题,相当数量仍然是典型题型,如何从多解走到最优解法、典型解法,这个路径比最终结果更加重要。
以广州一模为例,有三个层次。
6、7、8为代表,对高考真题很熟悉,在学习中已经锤炼过一题多解,才能在现场找到最优方案。
11、13、14为代表,对创新有联想、联系的解题习惯,能够找准突破口,也能在不利形势下找到证伪、验算等等的另辟蹊径。
17、18、19为代表,在直观想象、逻辑推理、抽象概括等数学思维上有充分的锻炼,既有实操,也能应变——这时候,在草稿纸上多做点推理、探索和猜想是有益的,绝不能提笔就写,绝不能赶这点时间。
对于大部分人来说,第一层能做到就很不容易了,很多人都知道要刷高考真题,但是什么样的值得深入,以及什么是典型解法、最优解法,这里面大有学问。
第二层,要求你不但多刷题、刷好题,还要多思考,绝不能偷懒,许多好题的复盘、分析、归纳、总结,都要自己真正走过,考场上才有可能产生这种联想联系。
第三层,如果你的目标是解答题第二问,那就不需要这么高的要求,但是草稿纸上充分思考之后再动笔的好习惯需要从现在、从平时就养成,考场上虽然不能保证每道压轴题都能够迎刃而解,至少人是清醒的,全局观还在,能准确评估每道题的完成度和时间的分配。
从去年八月、十二月的调研考到今天的一模,考生的能力肯定是在进步的,但是成绩不一定能够单调递增。试卷的难度是考生无法控制的,更何况这张试卷在计算量上还叠满了Debuff。