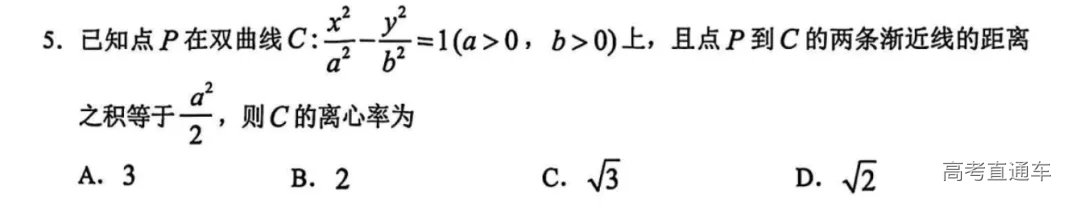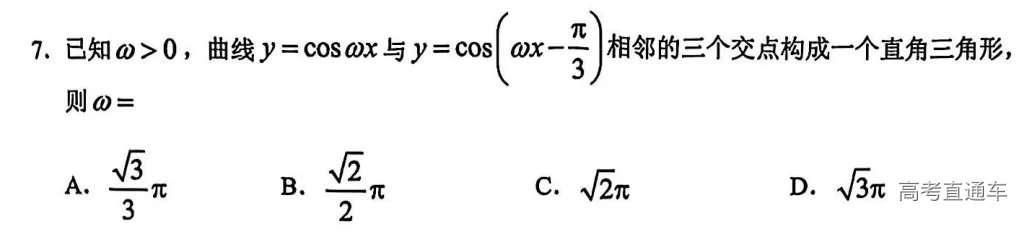今年数学试题整体难度偏大
但不少题目质量不错
属于“难但值得研究”的类型
你答对了吗?
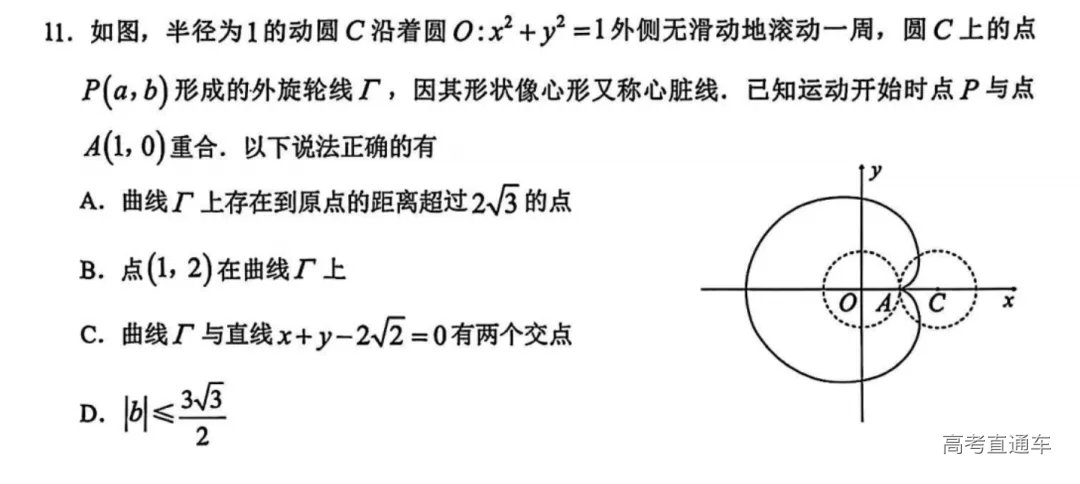
这道题算是基础送分题,基础薄弱的同学也很容易丢分。只要熟练掌握基础公式和几何关系,就能快速得出答案B,不需要深入分析或复杂推理。 直接应用公式:球的表面积、圆台侧面积公式均为基本几何公式 明确的几何关系:通过母线与底面的夹角直接关联高度、半径差和母线长。 无需复杂计算:所有步骤均为代数方程求解,无高难度变形或技巧。 这道题答案选D。题目设置的条件看似复杂,但通过以下步骤可简化为基本关系: 用距离公式表达条件,结合双曲线方程消元 通过对称性发现b²x²-a²y²=a²b²,直接代入化简 最终得到a=b,离心率e=√2,选项D 本题通过几何性质与代数运算的结合、隐含结论的应用、复杂条件的简化分析,全面考查考生对双曲线核心知识点的掌握。其亮点在于“形与数的统一”,要求考生既理解几何意义,又能熟练进行代数操作,最终指向离心率的本质——e=√1+b²/a²,充分体现数学思维的深度与灵活性。 这道题以“简洁条件”暗含“复杂逻辑”,通过符号分析、分类讨论、代数变形等核心方法,全面考查学生的数学素养。作为高考题改编,完美体现了三大特点: 一是知识整合,多板块知识点的无缝衔接,如指数函数、对数运算、不等式、代数方程等。 二是思维深度,从基础计算到高阶推理的梯度设计。基础层:直接应用对数公式alog3=blog4。进阶层:分析a与b的符号关系及大小差异。高阶层:通过分类讨论排除干扰选项,最终锁定唯一正确答案B。 三是命题技巧,通过选项陷阱和隐含条件,区分不同能力层次的学生。经典错误点:忽略负数场景(如误以为 a>b 在所有情况下成立);选项误导性:利用“倍数关系”(如 2b<a)制造思维惯性,考验学生的细致程度。 最终,只有选项B可能成立,其推导过程充分展现了数学的严谨性与灵活性,也符合高考选拔人才的核心理念。 这道题答案选A。题目将三角函数的周期性、相位差与几何直角条件结合,综合性较强。在解题过程中,考生需要利用图像来辅助理解,画出两个余弦函数的图像,观察它们的交点分布情况,以及如何形成直角三角形。掌握余弦函数的周期性、相位差公式及交点方程解法是考查重点。 本题答案是C。解题过程中需要综合应用函数性质、抽象不等式、数形结合、基本不等式的极值求解等知识。 本题选项ACD正确,题目通过极值条件、导数对称性、单调性分析、函数对称性四大维度,全面考查导数与原函数关系的应用。 本题答案为BCD,题目亮点在于通过动态几何模型将心脏线的生成过程与参数方程紧密结合,考察学生以下能力: 动态过程抽象:从滚动条件推导轨迹方程 多角度分析:利用代数、几何、极坐标方法验证选项 数形结合:通过动态图理解轨迹特性,避免纯计算误区 极值与范围求解:综合应用三角函数极值与不等式分析 答案是12种。本题既考察了排列组合的基本知识,又需要考生具备较强的逻辑推理和分步解决问题的能力,是典型的组合数学应用题。解题时,要通过系统化的列举和排除,确保所有可能的情况都被覆盖,同时验证其合理性。 答案是2π。这道题主要考查空间几何坐标定位与轨迹方程的综合分析能力。