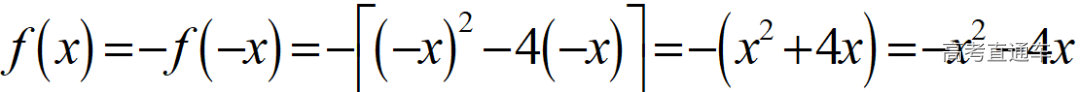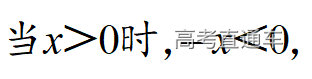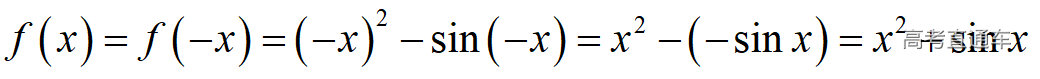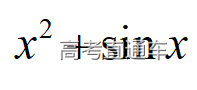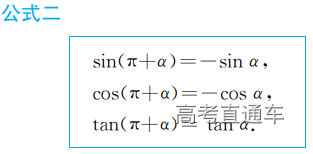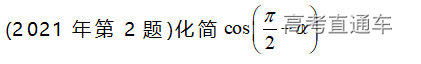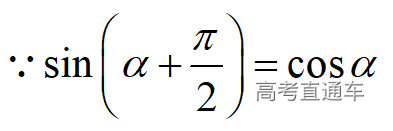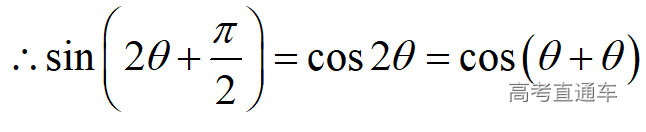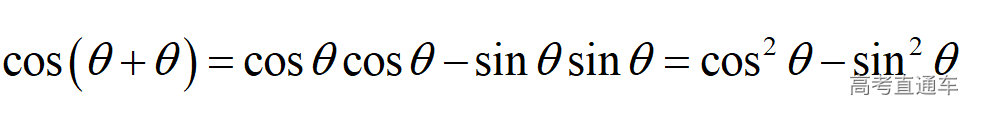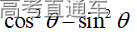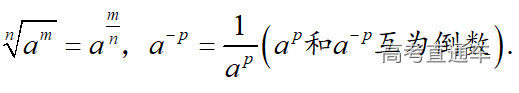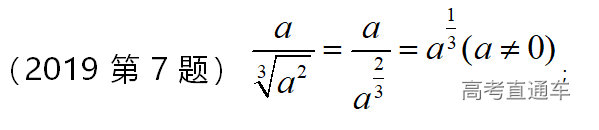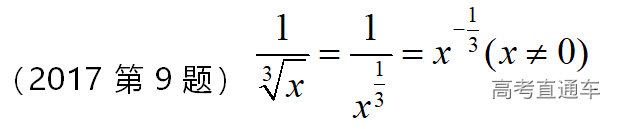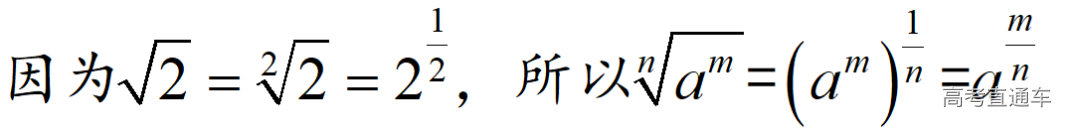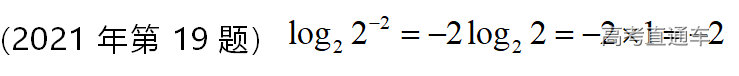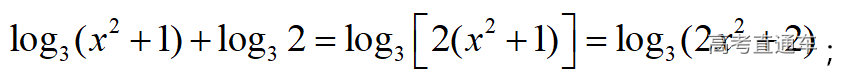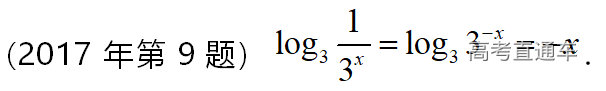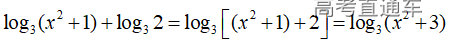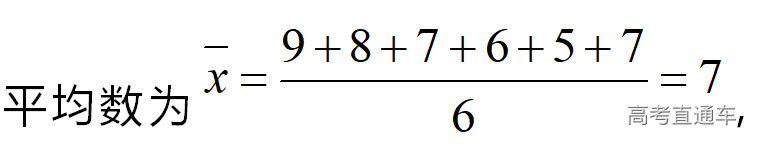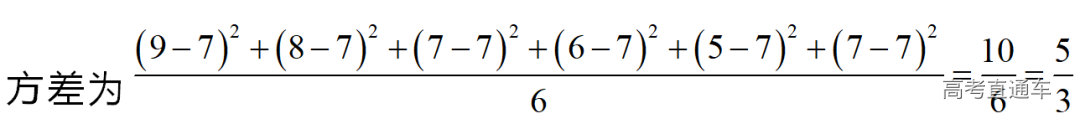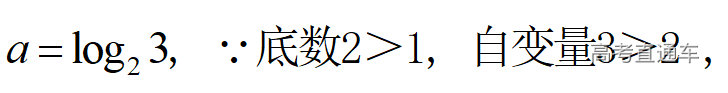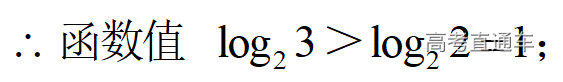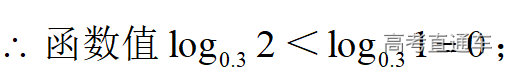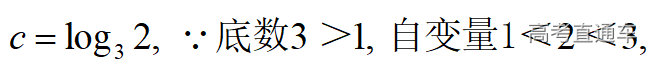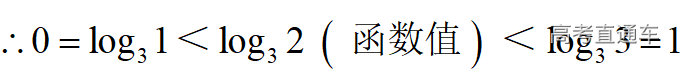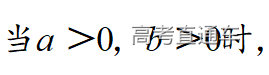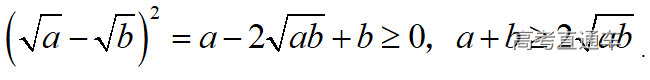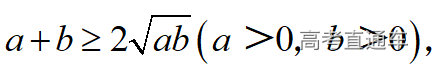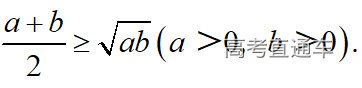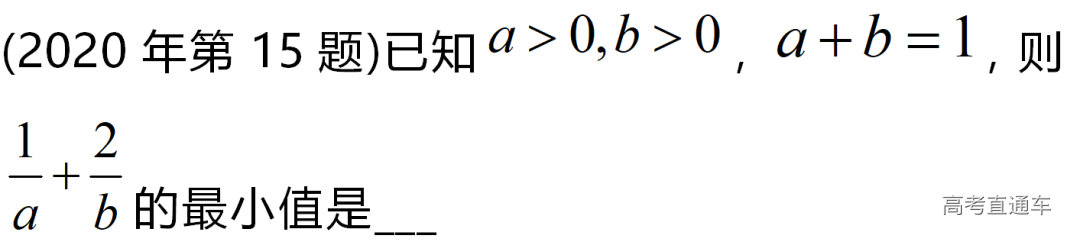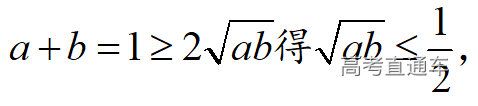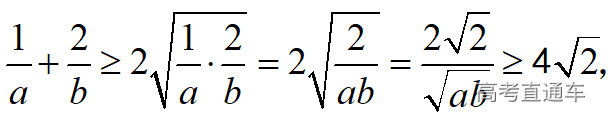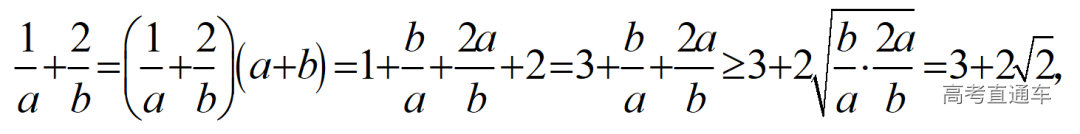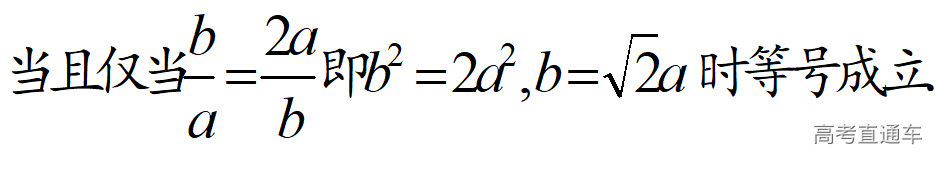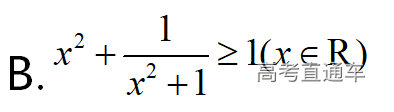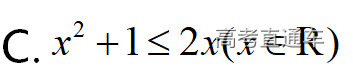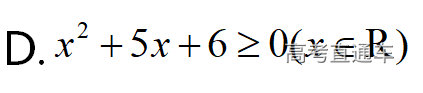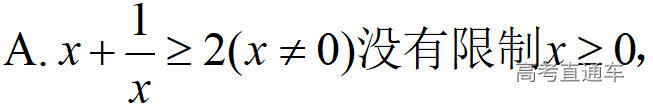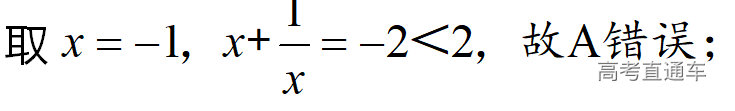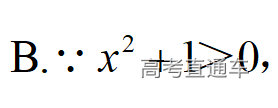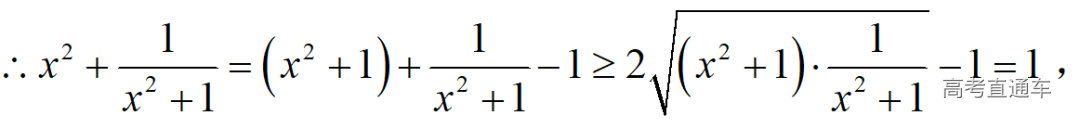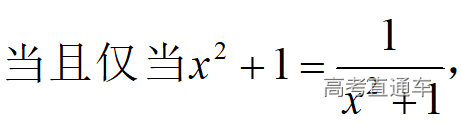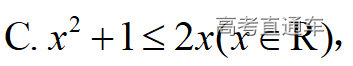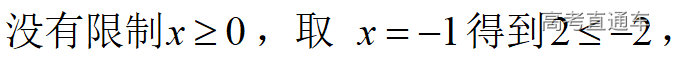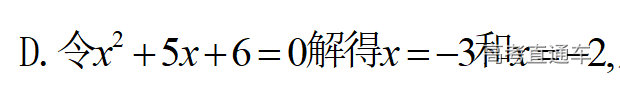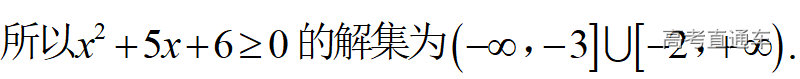“人非圣贤,孰能无过?”出错很正常,但是出了错,我们有必要分析出错的原因,尽量下次不出现同样的错误,只有这样才能不断地提高自己。下面来分析下学考数学真题的失分点,跟着小车一起来看看吧!
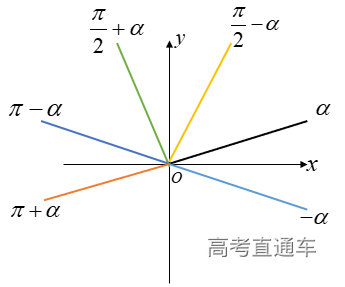
通常表现在概念不清、概念混淆或对概念的考点没有掌握全面等。下面我们以奇偶函数的概念为例来分析。 1.函数奇偶性的概念: (1)奇偶函数的定义域关于原点对称; (2)偶函数满足: 注意:偶函数和奇函数都是比较 【解析】 【答案】 【解析】 【答案】 【失分点剖析】 (1)没注意到:奇偶函数的定义域关于原点对称; (2)奇偶函数概念记不住或者混淆,为了准确记忆概念,我们可以去剖析概念的本质是在表达什么。 通常表现在没有掌握公式的化简过程;对公式的记忆不准确;对公式所表达的含义不理解等。下面我们来分析学考的重难点公式。 三角函数的诱导公式:诱导公式对于大家来说是重难点,建议画图来帮助理解记忆。 诱导公式说明: 【答案】 【解析】 【答案】 【失分点剖析】 诱导公式是重难点内容,学生对公式可能看不懂或者记不住,为了克服这个困难,可以总结化简步骤: (1)判断函数名是否改变; (2)判断符号。 2.分数指数幂的运算公式: 例如: 【失分点剖析】 (1) (2) 3.对数的运算公式: (1)牢记 (2)对数的运算常考的有加、减、幂的运算: 例如: 【失分剖析点】 不能正确的记忆应用公式,例如错记为 4. 平均数和方差公式: 一组数据为 例如:(2019年第8题)某地区连续六天的最低气温(单位:℃)为:9,8,7,6,5,7,则该六天最低气温的平均数和方差分别为_____. 【解析】 【答案】7, 【失分点剖析】 这个公式较长字母较多,不能理解公式所表达的内容;建议先理解公式里的字母表示的是什么,再通过练习去准确记忆。 通常表现在过程较多,思维难度较大,学生出现思维障碍;或者题目出现易错点,学生因为对知识内容掌握有漏洞等;最终导致失分。下面我们来分析思维失分的两道学考真题。 1.对数比较大小:底数大于1时,自变量越大函数值越大(不等号的方向不变);底数小于1时,自变量越大函数值越小(不等号的方向改变)。 例如,(2020年第11题) 2.基本不等式 推导: 内容: 即 注意: (1)不等式的使用条件是 (2)当且仅当a=b时等号成立. 【错误解法】 【失分点剖析】 解题过程中用了两次基本不等式,没有注意到这两次基本不等式的等号不同时成立: 【正确解法】考点:“1”的应用+基本不等式。 【解析】 【答案】 【解析】 故D错误。 【答案】B 【失分点剖析】 (1)没有注意: (2)没有注意: (3)不能通过灵活的变形来使用基本不等式。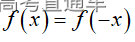
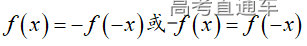
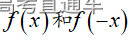
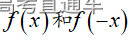
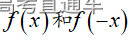


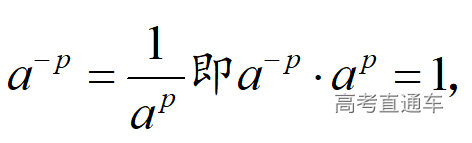
和
互为倒数。
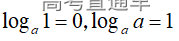
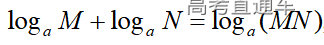
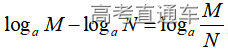
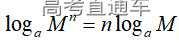
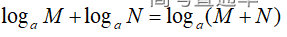
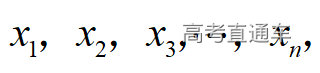
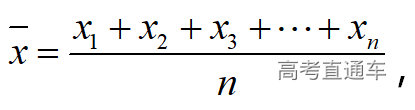
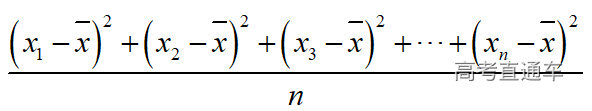
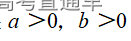
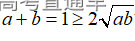
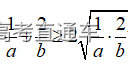
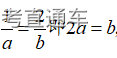
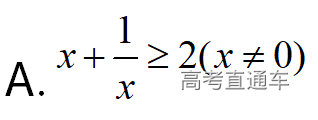
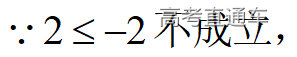
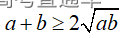
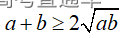
下面结合以上三类失分点,提出以下建议:
在基本的概念方面:首先要做到理解概念的内容,其次细节到概念的各个考点,最后通过运用准确记忆概念。
在重难点的公式方面:首先通过图象,举特例,总结口诀,理解公式中字母含义等方面理解公式所表达的内容;其次通过练习应用公式,从而熟能生巧;最后真正掌握这个公式。
在思维方面:对于较难的考点或题目,要总结思路,归纳方法,从而提高思维能力;对于易错的题目或者容易忽视的考点,要找出错误的原因并进行总结整理,时常翻看,从而避免此类错误。
“失败乃成功之母”,希望我们都能不怕困难,不怕失败,勇于尝试,最终取得自己的胜利!