典型例题分析1:
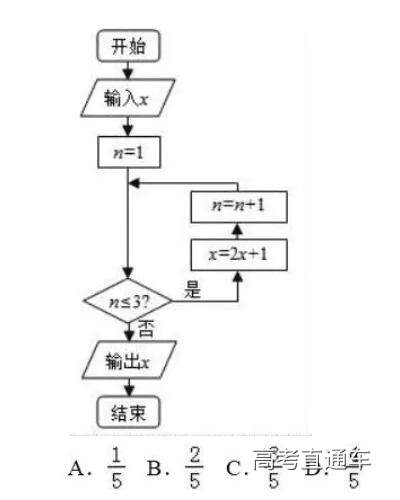
在闭区间[﹣4,6]上随机取出﹣个数x,执行如右图所示的程序框图,则输出的x不小于39的概率为( )
解:
由程序框图知,第一次循环,n=1,满足条件n≤3,y=2x+1,n=2,
第二次循环,n=2,
满足条件n≤3,y=2(2x+1)+1=4x+3,n=3,
第三次循环,n=3,
满足条件n≤3,y=2(4x+3)+1=8x+7,n=4,
此时不满足条件n≤3输出y=8x+7,
由8x+7≥39得x≥4,
即4≤x≤6,
则对应的概率P=(6-4)/(6-(-4))=2/10=1/5,
故选:A
考点分析:
几何概型;程序框图.
题干分析:
根据程序框图求出x的取值范围,结合几何概型的概率公式进行求解即可.
典型例题分析2:
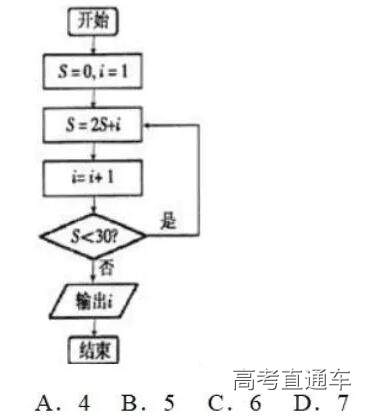
执行如图所示的程序框图,输出的i为( )
解:
由框图,模拟执行程序,可得:
S=0,i=1
S=1,i=2
满足条件S<30,S=4,i=3
满足条件S<30,S=11,i=4
满足条件S<30,S=26,i=5
满足条件S<30,S=57,i=6
不满足条件S<30,退出循环,输出i的值为6.
故选:C.
考点分析:
程序框图.
题干分析:
模拟执行程序,依次写出每次循环得到的S,i的值,当i=6时不满足条件S<30,退出循环,输出i的值为6.