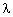,θ
,θ (0,π),则cotθ=________。
(0,π),则cotθ=________。 平方得
平方得 。
。 (0,π),
(0,π), ,
, 的两根。
的两根。 ,cosθ=
,cosθ= 。
。 ,应填
,应填 。
。 ],且x3+sinx-2a=0①,4y3+sinycosy+a=0②,求cos(x+2y)的值。
],且x3+sinx-2a=0①,4y3+sinycosy+a=0②,求cos(x+2y)的值。 ]上是单调奇函数,
]上是单调奇函数, ],
], ,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,则k的取值范围是______。
,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,则k的取值范围是______。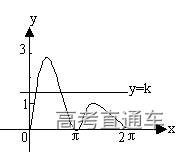
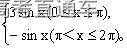
 ,x∈[0,2π]的图象(如图1)与直线y=k有且仅有两个不同的交点,则1<k<3。
,x∈[0,2π]的图象(如图1)与直线y=k有且仅有两个不同的交点,则1<k<3。 ,则tan2α=_________。
,则tan2α=_________。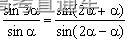
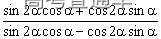
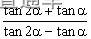
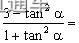
 ,
, =
= 。
。 为第四象限的角,
为第四象限的角, =
= ,
, =
= 。
。 ①,问此三角形是否可能为直角三角形?
①,问此三角形是否可能为直角三角形? ,
,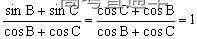
 ),
), 。
。 ,
, ,
, 。
。 ,
, ,
,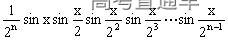
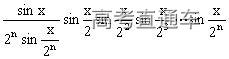
 。
。 。即原式得证。
。即原式得证。 。问f(x)是否是周期函数?若是,求出它的一个周期;若不是,请说明理由。
。问f(x)是否是周期函数?若是,求出它的一个周期;若不是,请说明理由。 的结构的形式极易与tan(x+
的结构的形式极易与tan(x+ )=
)= 进行类比,故可把tanx看成是f(x)的一个原型实例,且题中的λ相当于实例中的
进行类比,故可把tanx看成是f(x)的一个原型实例,且题中的λ相当于实例中的 。由于周期函数tanx的周期T=4·
。由于周期函数tanx的周期T=4· ,故可猜想f(x)也为周期函数,且周期为4λ。
,故可猜想f(x)也为周期函数,且周期为4λ。
 ,
,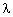 )=f[(x+2
)=f[(x+2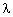 )+2
)+2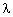 ]
] 。
。所以f(x)是周期函数,且4