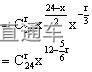二项式定理有关知识是常考内容之一。本文就二项式定理题型进行归纳总结,并对解法进行探讨,供参考。
知识点梳理
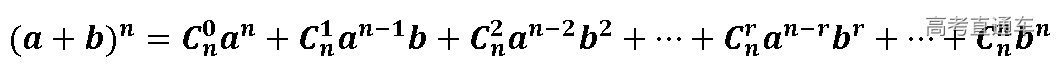
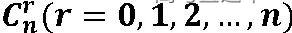
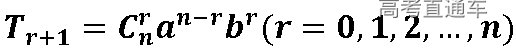
 是指展开式的第r+1项.
是指展开式的第r+1项.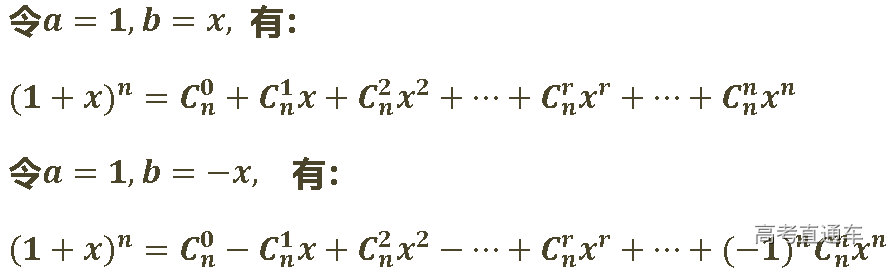

 中,最中间那一项(或最中间两项)的二项式系数最大。即:
中,最中间那一项(或最中间两项)的二项式系数最大。即:
 ,即:
,即: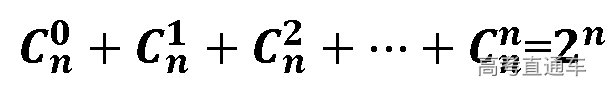
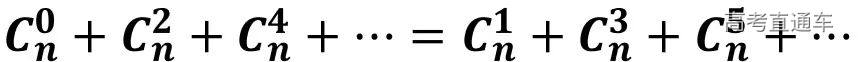
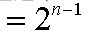
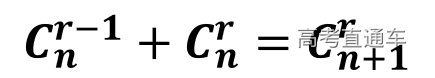
题型归纳
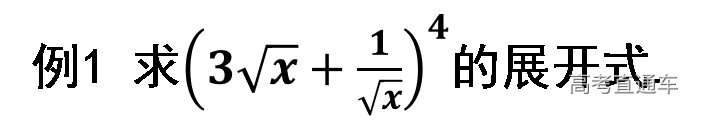
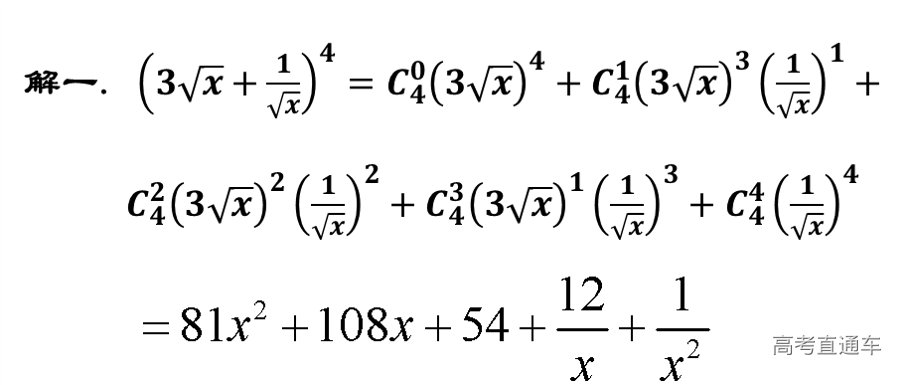
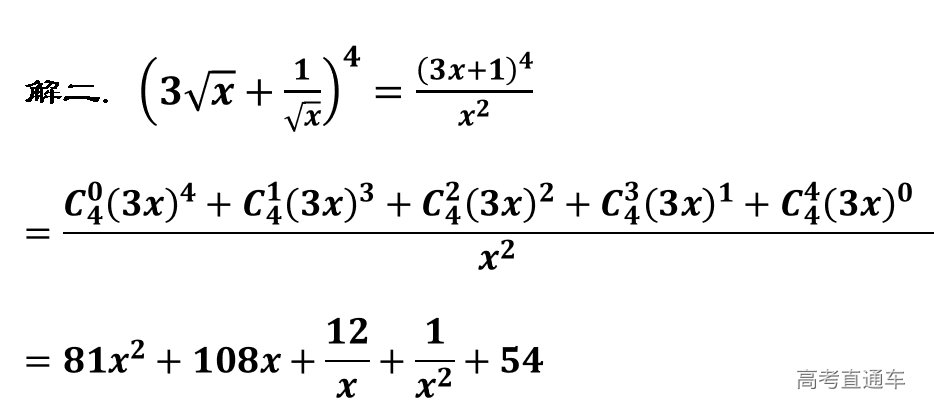


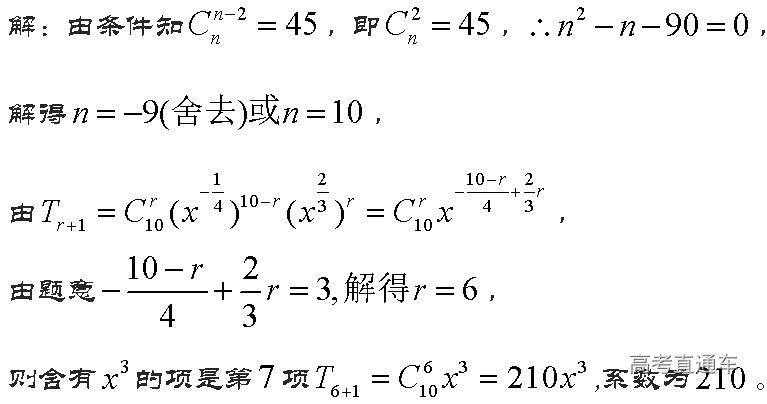
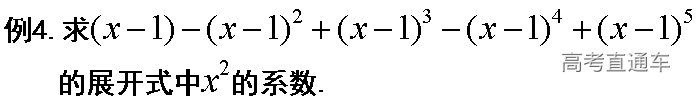

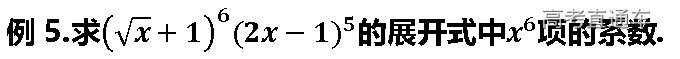

练习:
1. 求常数项
1、已知的展开式中第三项与第五项的系数之比为
,其中
,则展开式中常数项是( )
A. -45i
B. 45i
C. -45
D. 45
解析:第三项、第五项的系数分别为,由题意有
整理得
解得n=10
设常数项为
则有
得r=8
故常数项为,选D。
2. 求有理项
2、已知的展开式中,前三项系数成等差数列,求展开式中所有的有理项。
解析:展开式的前三项的系数分别为
则由题意可得
即
解得n=8(n=1舍去)
于是
若为有理项,则
,且
,所以r=0,4,8。
故展开式中所有的有理项为
3. 求幂指数为整数的项
3、在的展开式中,x的幂指数是整数的项共有( )
A. 3项
B. 4项
C. 5项
D. 6项
解析:
所以r=0,6,12,18,24时,x的幂指数为整数,故选C。
4. 求系数最大的项
4、已知的展开式中,只有第五项的二项式系数最大,求该展开式中系数最大的项。
解析:由只有第五项的二项式系数最大,可知展开式共有9项,故n=8
又
设第r+1项的系数最大,则有
解得
又,所以r=2或r=3
所以二项式的展开式中系数最大的项是
三、求展开式中系数和
在涉及到求展开式中所有项系数的和或者奇数项、偶数项系数和的问题时,通常可以根据题目的结构特征,选择“赋值法”来加以解决。
说明:系数和的问题,一般用赋值法,将式中的字母均赋值为1即可。
此种思路同样适用于底数为多项式的展开式。
说明:分奇偶项求系数和时,一般分别对变量赋值为1和-1,得方程组处理。
练习:若,
则=_____(用数字作答)。
解析:取x=0,得
取x=1,得
故
=2003+1=2004
四、求系数最大(最小)项
说明:系数最大或最小问题,一般可先设出最值项的项数,再利用不等式的恒成立性,求得系数最大或最小项。
也可将二项式看成数列,利用数列单调性的思路确定其单调性后处理。
五、多项展开式
有些三项式展开问题可以先通过变形转化为二项式展开问题加以解决,对于多项的和或积的二项式问题,可通过“搭配”解决,但要注意不重不漏。
说明:对于底数为多项式的展开式问题,如果能将底数变形为二项式,则直接用二项式定理;如果底数不能变形,可以采用上述三种方式处理。
其中解法三利用了多项式的乘法原理,更侧重于对二项式定理原理的理解和认识,应引起重视。
练习1、的展开式中整理后的常数项为________。
解析:
对于二项式的展开式中
要得到常数项需10-r=5,则r=5
所以常数项为
练习2、在展开式中,含
的项的系数是( )
A. 74
B. 121
C. -74
D. -121
解析:的展开式中,含
的项为
,故选D。
六、整除性问题
练习:已知数列和
的通项公式分别为
,将两个数列的公共项按它们在原数列中的先后顺序排成一个新数列
,求
的通项公式
。
分析: B被A整除可视,利用二项式定理将
表达式为
,若C可被A整数,则B可被A整除,可见提取公因式A乃关键所在。
解析:由于数列由数列
和
的公共项组成,那么必有
,即
,整理得
,则
必能被4整除。由二项式定理知:
,于是当且仅当
为奇数即
时,
才是整数,故
。
练习1:今天是星期天,从今天起天后的第一天是星期几?
分析:先考虑除以7的余数是多少,利用7天为一个周期的规律可推出结果,联想
便会找到解题思路。
解析:因为,而
可被4整除,所以
被7除的余数为4,从今天起
天后的第一天是星期五。
练习2:除以100的余数是___________。
解析:+92×90+1(M为整数)=100M+82×100+81。
所以除以100的余数是81。
七、近似计算
说明:在中学阶段,近似计算的处理,可以考虑二分法和二项式定理两种途径。
练习:求的近似值(精确到
)。
分析:凡二项式定理进行近似计算可根据精确度适当选用如下公式:,
。
解析:因为
,所以
。
八、证明不等式
说明:用二项式定理证明不等式,主要是利用其放缩的特征。
凡含有n次幂的不等式证明,可适当考虑此种思路。
练习1:已知是正整数,且
。证明:
。
证明:由二项式定理得:
,又
,所以
,故
。
练习2:已知,在
时,比较
与
的大小。
分析:使用换元策略转化问题,利用二项式定理将结论放缩到上来。
解析:因为,所以令
,于是
,故
。
九、求值
例17、用表示实数
的小数部分,若
,求
的值。
分析:挖掘倒数关系,并构造
是顺利解题的关键。
解析:设,则由二项式定理知:
,于是
必为正整数,故
,所以
。
十、与其它知识交汇型问题
在知识点的交汇处命题,已成为新高考命题的一个趋势。二项定理可以与组合、数列极限、杨辉三角等知识进行综合,而设计出新题。
例18、设常数a>0,展开式中
的系数为
,则
=___________________。
解:
由,得r=2
又
所以
另外,还有二项式定理与莱布尼茨三角形、极限的交汇题。