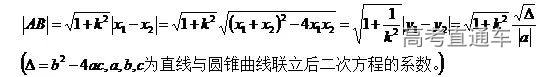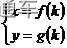推荐阅读：
直线与圆锥曲线是高考压轴大题中永远“绕不开”的考查点。
你是否曾被数不尽的参数、算不尽的Δ纠缠到快要崩溃？是否曾在计算了一整页草稿纸后却失望地发现计算错误？
椭圆，双曲线离心率公式和范围记不清，焦点分别在x轴，y轴上的双曲线的渐近线方程也傻傻分不清，在做题时自然做不对。计算能力强的同学在学圆锥曲线时相对轻松。可以尝试训练自己口算得到联立后的二次方程，然后得到判别式，两根之和，两根之积的整式。
圆锥曲线之所以难，是因为很多同学拿到题后觉得无从下手。实际上，大部分的圆锥曲线大题，都有共同的三部曲：一设二联立三韦达。- 一设：设直线与圆锥曲线的两个交点，坐标分别为（x1，y1），（x2，y2），直线方程为y=kx+b。
- 三韦达定理：得到二次方程后立马得出判别式，两根之和，两根之积。
走完三部曲之后，在看题目给出了什么条件，要求什么。例如涉及弦长问题，常用“根与系数的关系”设而不求计算弦长(即应用弦长公式)；涉及弦的中点问题，常用“点差法”设而不求，将弦所在直线的 斜率、弦的中点坐标联系起来，相互转化。总结起来：找值列等量关系，找范围列不等关系，通常结合判别式，基本不等式求解。- 若且a=0，b≠0，则直线与圆锥曲线相交，且有一个交点。
注意：设直线方程时一定要考虑斜率不存在的情况，可单独提前讨论。这类问题主要利用向量的相等，平行，垂直去寻找坐标间的数量关系，往往要和根与系数的关系结合应用，体现数形结合的思想，达到简化计算的目的。弦长问题主要记住弦长公式：设直线l与圆锥曲线C相交于A（x1，y1），B（x2，y2）两点，则：①定点问题可先运用特殊值或者对称探索出该定点，再证明结论，即可简化运算；
②直接推理、计算，并在计算推理的过程中消去变量，从而得到定值。几何法：若题目的条件和结论能明显体现几何特征和意义，则考虑利用图形性质来解决。代数法：若题目的条件和结论能体现一种明确的函数关系，则可首先建立起目标函数，再求这个函数的最值。在利用代数法解决最值与范围问题时常从以下五个方面考虑：①利用判别式来构造不等关系，从而确定参数的取值范围；②利用已知参数的范围，求新参数的范围，解这类问题的核心是在两个参数之间建立等量关系；③利用隐含或已知的不等关系建立不等式，从而求出参数的取值范围；轨迹问题一般方法有三种：定义法，相关点法和参数法。①分析题目：与动点M（x，y）相关的点P（x0，y0）在已知曲线上②寻求关系式，x0=f（x，y），y0=g（x，y）②得动点M的轨迹的参数方程 ![图片]()
④由k的范围确定x，y的范围，确保答案的准确性和完备性
这类问题通常先假设存在，然后进行计算，最后再证明结果满足条件得到结论。对于较难的题目，可从特殊情况入手，找到特殊点进行分析验算，然后再得到一般性结论。综上，考查直线与圆锥曲线，逃不过以相切、相交为切入点。
因此，计算相切时的直线方程、相交时的弦长就是这部分知识模块的必备技能。
针对这个疑难易错点，调研总结了直线与圆锥曲线相切及相交时的有关结论，助你理清思路，减少计算量，避免在解题时做无用功，加快解题效率。
1. 直线与圆锥曲线相切的有关结论
![图片]()
2. 直线与圆锥曲线相切的有关结论
![图片]()
本文来源高考直通车
