2022广州零模数学试题评析：难点突出，别出“新”裁

卓越教育高考改革研究委员会数学专家团队认为：今年的调研考风格与高考保持一致，考试内容及形式按照高考要求，难度相比于10月份的阶段训练考明显上升，能较好地检验学生一轮复习的效果，帮助学生对一轮复习查缺补漏，从而对二轮复习有更明确的方向。在题目内容的设计方面略有新意，本次考试多次出现对于最值问题的考查，注重学生对基础知识的综合运用与迁移能力。本文就2022届广州市高三调研考的设计、试题特点进行分析。

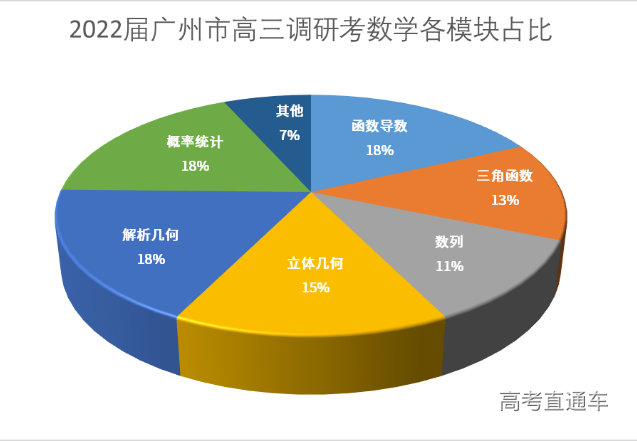
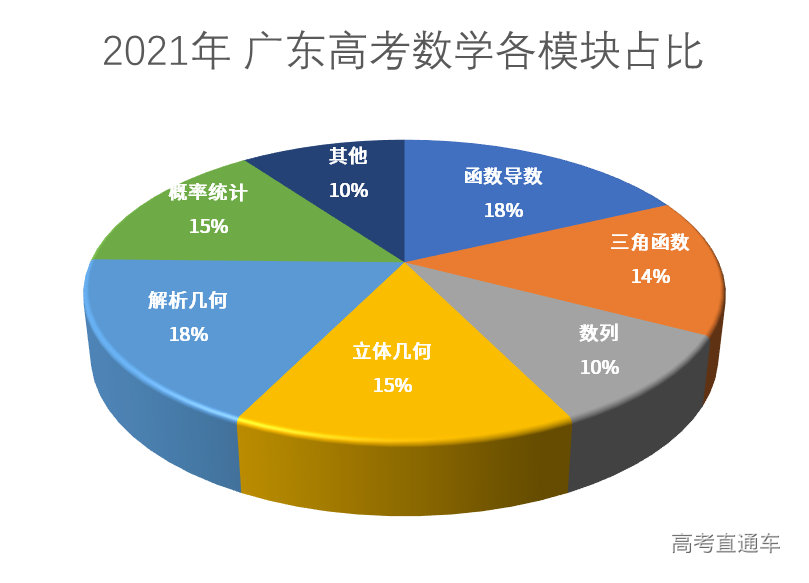
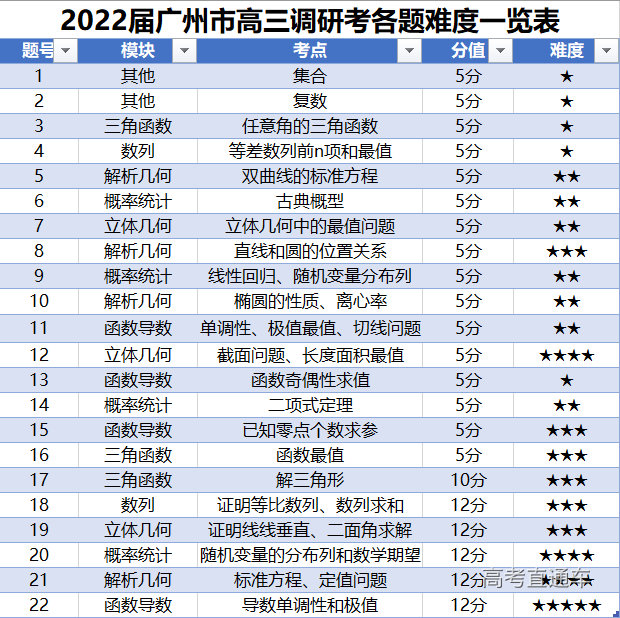
  由模块占比可知，试卷对六大板块的考查比重与去年高考基本一致，概率统计比重略有提升。在题目设置上注重对数学基础知识、数学思想方法和数学能力的考查。

选填题的整体难度偏基础，考点与新高考基本统一，题型设计也较为常规，覆盖面较广。对学生的数形结合能力与空间想象能力有一定要求。 

如第8题中的隐藏圆问题，第12题中立体几何的动点问题，16题的弧形与解三角形综合问题。另外，第5题将数学与实际生活相结合，与新高考的趋势统一，整体而言计算量不大。

其中，第8题考查了隐藏圆问题，考查了学生的抽象概括能力，转化与化归思想。其中也会涉及动点到圆的距离最值问题。

第12题考查了立体几何的动点问题，要求学生通过题目条件，通过展开图等方式，体现了对学生直观想象的素养要求。让学生充分运用空间想象能力，得到相关图形，本题关键在于明确动点在运动过程中的位置关系变化与线面角的变化。

第16题体现了推理论证与运算求解的能力，其中涉及到圆弧的基本性质、导数的综合应用。关键在于从题目条件中解读出面积的表达式，接下来可以通过基本不等式或者三角函数或者导数求最值，本题的入口比较宽，鼓励学生从不同的角度解决问题。

解答题考查的知识点模块与21年新高考Ⅰ卷一致，前4道解答题的顺序按难易程度有所调整，大部分题目考点比较常规，有部分题目设问方式比较新颖，凸显了基础性，综合性和应用性，能较好地检验学生目前阶段的复习成果。

第十七题为解三角形，考查了正弦定理的应用，并结合三角函数研究值域问题，检测了考生的数学应用能力和数学运算能力。本题更侧重于考察三角函数及平面向量的化简，题目难度不大，目的在于警示同学们不能忽略基础模块的复习。

第十八题为数列，考查了数列求和与通项间的基本关系，并结合等比数列求解通项公式，第二问中以插入数列方式呈现，比较有新意，实际是考查分组求和，建议同学们用枚举法分别数出两个数列所占的项数，检测了考生的逻辑推理能力和数学运算能力，虽然第二问设问具有一定创新性，但整体难度不大。

第十九题为立体几何，图形为经典的直三棱柱模型，考查了线线垂直的证明与二面角的求解，比较常规，检测了考生的直观想象能力和数学运算能力。第一问需要多次使用勾股定理求出棱长及确定垂直关系，第二问用建系的方式能较好解决，唯一的难点是求出点D的坐标，只要计算基本功扎实，相信问题不大。

第二十题为离散型随机变量，第一问考查基础离散型随机变量数学期望的计算，第二问而需用函数思想研究二项分布概率的最值，需要结合导数研究函数的最值，检测了考生的数学应用能力和数学运算能力，符合新高考对于考生核心素养的要求。类似结合导数的概率统计解答题，2018年新课标Ⅰ卷曾出现过。

第二十一题为圆锥曲线，本题出题背景为2014年广东卷出现过的蒙日圆的双切线垂直性质，考查了椭圆的方程与定值问题。第一问结合椭圆定义求方程比较常规，第二问中的定值探究问题，学生可以先从斜率不存在的特殊情况探究出两个向量数量积为零，为后续把向量垂直问题转化为斜率关系建立基础，减少一定的计算量，另一难点在于引入字母较多，计算比较繁杂，需要合理应用变换主元思想，对运算能力要求较高。

第二十二题为导数，考查了利用导数研究函数的性质。本题难度与高考真题难度相仿，符合高三一轮复习的学生现阶段的学情。第一问较常规，考查了利用导数研究函数的单调性，比较常规。第二问重点考查双变量问题，一般可有两种转化为单变量的方式，既可以通过韦达定理消元处理，也可以采用整体比例换元法处理，都体现了把双变量转化为单变量的思想，通过构造新函数研究函数的最值，体现了试题的开放性。

总体来说， 本次考试强调数学思想的应用，重点突出对于必备知识的考查，指导学生在接下来的高考复习当中不仅需要重视基础知识的储备，也要提升知识迁移应用的能力。

高考复习尚未结束，同学们仍有很大的提高空间，万不可因一次考试而灰心丧气或骄傲自满。

回归课本，从教材例题深挖，结合公式定理、概念知识，搭建完备的知识框架，做到“吃透课本、抓实基础、注意通法通解，理解中心思想”。

在备考过程中，应增强题组训练，熟练解题模板；应增加限时训练，加快做题速度，以更好地应对后续的学习与考试，迎战高考！